1) Lagrangian equations


拟拉格朗日方程
2) Lagrange equation


拉格朗日方程
1.
The motion mathematical model is established for the lifting system by using Lagrange equation and is used to numerically simulate the dynamic response of the lifting system.
为研究铰接式扬矿系统的动态影响,分析了波浪液动力、流体阻力和流体附加质量对多段铰接式连接扬矿系统的影响,采用拉格朗日方程建立系统的运动数学模型,并对系统的运动响应进行数值模拟;计算结果和实验基本相符。
2.
With quadratic lagrange equation, large , medium and small of kinds differential equation of movement are established; Solution of equation is calculated and approximately per-formed , and qualitative explanation and quantitative analysis are made.
利用二阶拉格朗日方程,建立起大、中、小三类提升机的运动微分方程;并对其解进行了演算与近似演算,做出了定性说明和定量分析。
3.
The dynamic equations of the couple pendulum near the balance location were given by using Lagrange equation.
利用保守系的拉格朗日方程,给出了耦合摆在平衡位置附近的动力学方程,求解出耦合摆在平衡位置附近作小振动时的本征频率。
4) Lagrangian equation


拉格朗日方程
1.
Study on State Feelback Control of Car-seesaw Based on Lagrangian Equation;


基于拉格朗日方程的小车跷跷板状态反馈控制研究
2.
In this paper,the typical multi-variable and nonlinear Ball-Beam System is studied,and its mathematic model is constructed with Lagrangian equation and a related controller is designed with the state-feedback method of modern control theory.
以典型多变量非线性系统——球棒系统为研究对象,用拉格朗日方程建立其数学模型,并用现代控制理论中的状态反馈的方法设计该非线性系统的控制器。
3.
In this paper,we study the typical multi-variable and nonlinear Ball-and-Beam System, construct its mathematic model by Lagrangian equation and design its controller by state feedback of modern control theory.
以典型多变量非线性系统———球棒系统为研究对象,用拉格朗日方程建立其数学模型,并用现代控制理论中的状态反馈的方法设计该非线性系统的控制器。
5) Lagrange equations


拉格朗日方程
1.
Establish the several degrees-of-freedom model of this pendulum by using the Lagrange equations,and the model is linearized at the balance state.
对于此钟摆现象,采用拉格朗日方程建立其多自由度模型、并在平衡态进行解耦和线性化。
2.
Based on Lagrange equations,a dynamic model is derived for typical underactuated mechanical gantry crane system.
针对龙门吊车这一典型的欠驱动机械系统,采用拉格朗日方程的方法建立了其动力学模型。
3.
A simple method of deriving accelerations in orthogonal curilinear coordinates is proposed by using of Lagrange equations.
采用拉格朗日方程,给出一种求解正交曲线坐标系中加速度的简捷方法。
6) TL formulation


全拉格朗日方程
补充资料:拉格朗日方程
| 拉格朗日方程 Lagrange equation 对完整系统(见约束)用广义坐标表示的运动微分方程组,通常指第二类拉格朗日方程。简称拉氏方程。由J.-L.拉格朗日首先导出而得名 。可写为 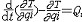 (i=1,2,…,N),式中T为用各广义坐标qi和广义速度qi表示的系统的动能;Qi为对应qi的广义力。方程式的个数等于系统的自由度N。保守系统中存在势函数V(q1,q2,…,qN;t),则广义力 (i=1,2,…,N),式中T为用各广义坐标qi和广义速度qi表示的系统的动能;Qi为对应qi的广义力。方程式的个数等于系统的自由度N。保守系统中存在势函数V(q1,q2,…,qN;t),则广义力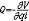 ,又因V中不含qi,即 ,又因V中不含qi,即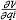 =0,故完整保守系统的拉格朗日方程为 =0,故完整保守系统的拉格朗日方程为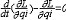 (i=1,2,…,N),式中L=T-V为拉格朗日函数,又称动势,它等于系统的动能与势能之差。上式与变分问题中的欧拉方程形式相同,由此可导出哈密顿原理。若已知系统的动能和作用于该系统的广义力,或已知系统的拉格朗日函数,则可从拉氏方程解出广义坐标作为时间的函数即系统的运动规律。拉氏方程采用广义坐标,对有约束的系统,其广义坐标一定比直角坐标个数少,从而拉氏方程的数目比牛顿方程少,方程总阶数也较低,易于求解。由于拉氏方程中不包含约束力,并可根据约束条件适当选择广义坐标,因而可简化求解质点系动力学的问题,约束力可在拉氏方程解出后再用牛顿方程求出。 (i=1,2,…,N),式中L=T-V为拉格朗日函数,又称动势,它等于系统的动能与势能之差。上式与变分问题中的欧拉方程形式相同,由此可导出哈密顿原理。若已知系统的动能和作用于该系统的广义力,或已知系统的拉格朗日函数,则可从拉氏方程解出广义坐标作为时间的函数即系统的运动规律。拉氏方程采用广义坐标,对有约束的系统,其广义坐标一定比直角坐标个数少,从而拉氏方程的数目比牛顿方程少,方程总阶数也较低,易于求解。由于拉氏方程中不包含约束力,并可根据约束条件适当选择广义坐标,因而可简化求解质点系动力学的问题,约束力可在拉氏方程解出后再用牛顿方程求出。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条