1) non-onesided bouneded variation sequence(NBVS)


双边有界变差数列
2) non-one sided bounded variation sequence condition


双边剩余有界变差条件
3) piecewise bounded variation sequence


分段有界变差数列
1.
We generalize some classical results in convergence and integrability for the trigonometric series with non-negative coefficients to the series with varying coefficients (they may change signs),by introducing the so-called piecewise bounded variation sequences (PBVS).
通过引入所称谓的分段有界变差数列(PBVS),将关于具有非负系数的三角级数的收敛性和可积性的经典结果推广到具有可变系数(允许变号)的三角级数。
4) Rest bounded variation sequence


剩余有界变差数列
5) mean value bounded variation sequence


均值有界变差数列
6) Kth order weak bounded variation function


叙列空间上的K级弱有界变差函数
补充资料:有界变差函数
| 有界变差函数 bounded variation,function of 定义在区间[a,b]上,并能表为两个单调增函数之差的实值函数。属常用的函数类,它有许多好的性质,例如:有界变差函数必为有界函数;两个有界变差函数的和、差、积仍为有界变差函数;有界变差函数在[a,b]上黎曼可积;有界变差函数在[a,b]上几乎处处可导,导函数在[a,b]上勒贝格可积。此外还有,平面上由y=f(x)表示的曲线C可求长的充分必要条件是f为有界变差函数。应注意的是,连续函数不一定为有界变差函数。例如: 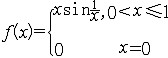 。 。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条