1) space of special functions with bounded deformation


特殊有界形变函数空间
2) BD(Ω)


有界变差函数空间BD(Ω)
3) M-1-variation function space


M-1-有界变差函数空间
4) Kth order bounded variation function space


K级有界变差函数空间
5) Kth order weak bounded variation function


叙列空间上的K级弱有界变差函数
6) Bounded Mean Oscillation Function Space


有界平均振动函数空间
1.
Bounded Mean Oscillation Function Spaces for Nondoubling Measures;


非二倍测度条件下有界平均振动函数空间
补充资料:函数空间
| 函数空间 functional space 由定义在一般集合上的函数组成的集合,并且在 集合中装备了一定的几何结构。例如取X={f∶f为定义在[a,b]上的连续函数}, 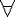 f∈X,定义‖f‖= f∈X,定义‖f‖=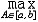 |f(t)|,称之为f的范数,范数是通常长度概念的拓广 ,利用范数可定义X中任何两个元素(或点)之间的距离ρ(f,g)=‖f-g‖,则X就是一个函数空间,在X中可以谈论点列(即函数列)的收敛问题:{fn} |f(t)|,称之为f的范数,范数是通常长度概念的拓广 ,利用范数可定义X中任何两个元素(或点)之间的距离ρ(f,g)=‖f-g‖,则X就是一个函数空间,在X中可以谈论点列(即函数列)的收敛问题:{fn}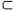 X,f∈X,fn→f,当且仅当ρ(fn,f)=‖fn-f‖= X,f∈X,fn→f,当且仅当ρ(fn,f)=‖fn-f‖=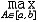 |fn (t)-f(t)|→0 。此外,还可在X中规定加法和数乘运算如下 : |fn (t)-f(t)|→0 。此外,还可在X中规定加法和数乘运算如下 :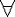 f ,g∈X, α∈IR,则定义(f+g)(t)=f(t)+g(t),(αf)(t)=α·f(t),则 X是一个线性空间,事实上X为一完备的线性赋范空间,即巴拿赫空间。常用的函数空间不一定有以上空间那样好的性质,但一般来说为线性拓扑空间,空间中的元素不仅满足线性关系,并且线性运算关于拓扑是连续的,有可能研究连续、有界、可微等分析性质。 f ,g∈X, α∈IR,则定义(f+g)(t)=f(t)+g(t),(αf)(t)=α·f(t),则 X是一个线性空间,事实上X为一完备的线性赋范空间,即巴拿赫空间。常用的函数空间不一定有以上空间那样好的性质,但一般来说为线性拓扑空间,空间中的元素不仅满足线性关系,并且线性运算关于拓扑是连续的,有可能研究连续、有界、可微等分析性质。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条