1) manifold
[英]['mænɪfəʊld] [美]['mænə'fold]
流形
1.
Multi-manifold learning using locally linear embedding (LLE) nonlinear dimensionality reduction;
基于局部线性嵌入(LLE)非线性降维的多流形学习
2.
On Submanifolds with Parallel Mean Curvature Vector in Riemannian Manifolds;
黎曼流形中具有平行平均曲率向量的子流形
3.
Expansion Model Based on Multi-manifold for Nonlinear System;
非线性系统多流形展开模型
2) manifolds
[英]['mænifəuld] [美]['mænə,fold]
流形
1.
Brittleness theory analysis of complex system on manifolds;
流形上复杂系统的脆性理论分析
2.
The results show that the fundamental reason for the occurrence of voltage collapse is due to the non transversal intersection between solution manifolds of the injection branch equations of generators and loads and the linear electrical network equations in the bus voltage and injection current space.
文中细致地研究了基于物理电路方程解流形的电压崩溃机理。
3.
The structure of manifolds near collinear Lagrange points changes under small perturbations.
对影响空间探测任务的三个共线平动点的稳定性进行了分析,得出了共线平动点不稳定的结论,在小的扰动下平动点附近的流形就会发生结构性的变化;其次,以空间围绕拉格朗日点的周期轨道为基础研究了日地三体模型和地月三体模型下空间的流形的走向和形态,对于由周期轨道生成的空间流形构成的管状通道进行了分析。
3) Configuration manifold
位形流形
4) Formal Generic manifold
形式Generic流形
5) Egg shape submanifold
卵形子流形
6) streamline topographic form
流线形地形
补充资料：流形
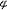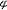| 流形 manifold 一类特殊的连通、豪斯多夫仿紧的拓扑空间。在此空间每一点的邻近预先建立了坐标系，使得任何两个（局部）坐标系间的坐标变换都是连续的。这里所说在一点邻近建立坐标系就是：存在这个点的一个邻域U和一个同胚映射  ：U→V，其中V是某个欧氏空间Rn中的开集。这样的 可看成U上n个函数，它们就给出U中点的坐标。在上面流形的定义中，若坐标变换皆是连续可微的，则进一步称空间为微分流形。流形的概念最早是由B.黎曼在1854年提出的。流形最重要的特性是：有局部坐标系。这个特性并不奇特，以至流形能广泛地出现在物理、几何问题之中。同时这个特性又使人们可系统地运用坐标方法，从而导致富有成效的研究。因此流形成为数学中一个重要概念。 对流形的研究还有一套组合方法，H.庞加莱对这种方法的出现起了决定性作用。那是预先假定流形“剖分”成一些单形之和，使各单形之间是规则相处的。从“剖分”出发，创造出链群和边缘算子概念，再用有限的代数算法导出同调群，进而开展研究（见同调论）。 关于流形的重要结果有：斯托克斯公式，示性类，德·拉姆同构，对偶定理。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条