1) dyschromatosis symmetrica hereditaria
遗传性对称性色素异常症
1.
Six novel mutations of ADAR1 gene with dyschromatosis symmetrica hereditaria;
遗传性对称性色素异常症6个新的致病基因突变研究
2.
Detection of mutation of DSRAD of a patient with atypical vitiligo in a family of dyschromatosis symmetrica hereditaria;
遗传性对称性色素异常症一家系中不典型白癜风患者1例
3.
Background Dyschromatosis symmetrica hereditaria (DSH, 0MIM#127400) is an autosomal dominant pigmentary genodermatosis characterized by hyperpigmented and hypopigmented macules of on the extremities.
遗传性对称性色素异常症(DGH，OMIM#127400)是一种以肢端对称分布色素沉着和色素减退斑为特怔的常染色体显性遗传病，婴儿期或儿童期发病，在亚洲人中较常见。
2) Dyschromatosis symmetrical hereditaria
遗传性对称性色素异常症
1.
Study on Clinical Character and Genetic Model of Dyschromatosis Symmetrical Hereditaria and Freckle;
遗传性对称性色素异常症和雀斑的临床特点和遗传方式研究
3) DSH
遗传性对称性色素异常症(DSH)
4) dyschromatosis symmetrica hereditaris
遗传性对称性肢端色素异常
5) dyschromatosis universalis hereditaria
遗传性泛发性色素异常症
1.
One case of dyschromatosis universalis hereditaria;
遗传性泛发性色素异常症1例
6) symmetry inheritance
对称性遗传
补充资料：(3)对称性
(3)对称性
(3)symmetry强子之间存在的一种包括同位旋对称性和超荷对称性在内的更高的内部对称性。这个对称性表明，所有的强子可以分成若干组，组内的粒子有相同的时空对称性质（例如自旋、宇称）和重子数，有比较接近的静质量，有各不相同但按一定规律分布的同位旋 (
)、同位旋投影(
)量子数和超荷值(
),它们在相互作用过程中表现出大体上一致、彼此密切相关的性质。利用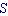 
(3)群这一数学工具来描述强子之间的这种对称性质，研究粒子的分类、基本属性以及它们在各种相互作用过程中的互相关联的理论称为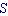(3)对称性理论。历史 随着科学技术的进步，人们制造和探测高能粒子的手段不断更新，发现的新粒子、新现象越来越丰富。20世纪50年代确立了一系列奇异粒子，60年代又陆续发现了为数众多的共振态粒子，使得当时已发现的粒子（主要是强子）的数目猛增至一二百个之多，大大超出了发现元素周期律时已发现的化学元素的数目。在这种情况下，把这么许多粒子进行科学的分类，找出它们性质之间的内在联系，并进而追溯这些联系的根源，就成了当时十分迫切的课题。
在这样的基础上，60年代前期，经过许多科学工作者的共同努力，包括大量深入的理论探索和细致周密的实验分析，揭示了强子的
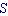
(3)对称性，利用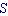(3)群把同位旋对称性和超荷对称性结合起来，统一到一个更大更高的内部对称群中去，发展并最后确立了关于强相互作用粒子的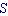(3)对称性理论。强子
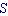
(3)对称性的建立 利用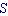(3)群来研究强子对称性的早期尝试,与强子结构的坂田模型密切相关
50年代初，高能物理中发现了一系列奇异粒子，引入了奇异数，并总结出了著名的盖耳-曼-西岛法则。在此基础上日本物理学家坂田昌一在1955年提出了坂田模型，假定所有的强子都是由质子(p)、中子(n)和
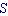
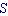
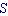
超子以及它们的反粒子组成的。正像忽略去质子和中子的差别以后核力和核子体系具有同位旋对称性[即 (2)对称性]一样，如果人们忽略 粒子与核子之间的差异，而把它们看作同一粒子所处的三种不同状态，它们之间应具有(3)对称性，由它们所构成的强子体系也应具有(3)对称性。按照李群的基本理论,
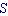
(3)群的不可约表示可以用一对非负整数(
，
)来标志，记作
(，),通常用黑体的维数数字来代表，例如：(0,0)＝1，(1,0)＝3，(0,1)＝3
，(1,1)＝8，其中3是3的共轭表示。在
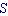
(3)变换下,基本的(p，n，)具有重子数
＝1，按基础表示3变换,[kg2]
相应的反粒子(
，
，
)具有重子数＝-1，按共轭表示3变换。按坂田模型,＝0的介子由一对正反(p，n，)组成，它们应按表示8和1变换当时实验上已确认的赝标介子只有同位旋三重态的普通介子(
,
,
)和两个同位旋双重态的奇异介子(K，K和K,[kg2]
),它们一共有七个根据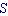(3)对称性预言至少应当存在一个同位旋单态的普通介子，与上述七个粒子组成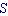(3)八重态不久果然在实验上发现了单态非奇异介子
(548)。与赝标介子的情形相似，先后在实验上发现的矢量介子
(，，)、K(K, K；K,)、ω和
一共九个,适合于填充可约表示 8+1可见,以坂田模型为基础的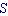(3)对称方案很好地解释了介子的性质。但是，坂田模型关于重子的分类方案却遇到了原则性的困难。例如，重子数
＝1超荷＝0的Σ超子三重态可能填充的不可约表示是6或15但6中根本没有另一个超子(=-1的双重态)Ξ的位置；而15中虽然可以容纳Ξ超子，却还预言许多至今都没有任何迹象的空额粒子。1961年在重新仔细分析实验资料的基础上,M.盖耳-曼和Y.奈曼提出了新的八重态分类方案（称为八重法），假定八个重子（N,Ξ,Σ和
）和八个赝标介子(K,,和)一样,[kg1]
属于不可约表示8。按照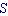(3)群表示的乘法规则，主要衰变为一对赝标介子的矢量介子共振态和主要衰变为一个赝标介子和一个 [902-01]
重子的[902-02]
重子共振态都应当属于不可约表示27,10,10,8或1。
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条