1) Montgometry's sieve


Montgomery 筛法
2) Montgomery algorithm


Montgomery算法
1.
Montgomery algorithm on elliptic curves over finite fields of character three;


特征3有限域上椭圆曲线的Montgomery算法
2.
Works at the common generating algorithms,that is,certain generating algorithms and probabilistic generating algorithms,and demonstrates a programming algorithm based on Miller-Rabin algorithm improved by Montgomery algorithm and Pocklington .
文中在研究了密钥生成的一般算法的基础上,即确定性素数产生和概率性素数产生方法,给出了利用Montgomery算法优化的Miller-Rabin算法和Pocklington定理算法实现,构造了大素数的生成算法,以提高RSA算法的安全性和运行速度。
3.
Montgomery algorithm is a fast modular multiplication algorithm and is widely used in the base operation of public-key cryptography algorithms such as RSA and ElGamal.
Montgomery算法作为一种快速模乘算法,常被应用于RSA、ElGamal等公钥密码算法的基本运算。
3) Montgomery modular inverse


Montgomery 逆算法
1.
After a comprehensive investigation of the Montgomery modular inverse algorithm and its refined versions, we present two modified high radix algorithms.
本文通过对 Montgomery 逆算法核心部分的改进,得到两种分别以4为基和8为基的优化算法。
4) Montgomery point multiplication


Montgomery点乘法
5) Montgomery multiplication


Montgomery模乘算法
1.
This paper proposes a modified multiple-word radix-2k Montgomery multiplication(MWR2kMM) algorithm with its corresponding VLSI architecture.
在改进基于字的Montgomery模乘算法的基础上,通过优化流水线结构缩短关键路径,实现了一种结构优化的模乘器。
2.
This paper presents an optimized architecture of a scalable radix-4 modular multiplier,based on radix-4 Montgomery multiplication algorithm and improved pipeline architecture.
基于基为4的Montgomery模乘算法和改进的流水线组织结构,文章提出了一种结构优化的可扩展模乘运算器结构。
6) Montgomery square


Montgomery平方算法
补充资料:筛法
| 筛法 sieve method 在数论中有广泛应用的一个初等数学方法。起源于古老的埃拉托斯特尼筛法,这个古老筛法是选出不超过N的素数表的方法,它基于下述一个简单结果如果n≤N, 且n是复合数,则n必为一个不大于 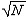 的素数所整除 ,具体做法如下:先列出不大于 的素数所整除 ,具体做法如下:先列出不大于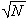 的全体素数 ,记为 2=p1<p2<…<pr≤ 的全体素数 ,记为 2=p1<p2<…<pr≤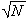 ,然后依次写出整数2,3,4,…,N,在其中留下p1=2,然后把p1的倍数全划掉,再留下p2=3,而把p2的倍数全划掉,继续如此往下做 ,直到最后留下pr,而把pr的倍数全划掉,最后所留下的整数就是不超过N的全体素数。埃拉托斯特尼筛法的改进和发展,成为近代解析数论的重要工具。例如V.布龙在 1920年对上述古老筛法做了重要改进,证明了命题(9,9)。这里命题(a,b )表示每个足够大的偶数都可以表成两个正奇数之和,而这二个奇数所含素因子个数分别不超过a和b,这是对哥德巴赫猜想研究的重要贡献。他的方法称为布龙筛法。以后筛法又得到进一步改进,相继提出所谓罗塞筛法,塞尔伯格筛法和大筛法等。 ,然后依次写出整数2,3,4,…,N,在其中留下p1=2,然后把p1的倍数全划掉,再留下p2=3,而把p2的倍数全划掉,继续如此往下做 ,直到最后留下pr,而把pr的倍数全划掉,最后所留下的整数就是不超过N的全体素数。埃拉托斯特尼筛法的改进和发展,成为近代解析数论的重要工具。例如V.布龙在 1920年对上述古老筛法做了重要改进,证明了命题(9,9)。这里命题(a,b )表示每个足够大的偶数都可以表成两个正奇数之和,而这二个奇数所含素因子个数分别不超过a和b,这是对哥德巴赫猜想研究的重要贡献。他的方法称为布龙筛法。以后筛法又得到进一步改进,相继提出所谓罗塞筛法,塞尔伯格筛法和大筛法等。中国的数学家对筛法的理论和应用有重要贡献。1957年王元证明了命题(2,3),1962年潘承洞证明了命题(1,5),1966年陈景润证明了命题(1,2),陈景润的详细证明在1973年发表后,世界公认这是筛法理论的最卓越的应用成果。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条