2) particle size distributional fractal dimension


粒度分布分形维
1.
Study on relationship between particle size distributional fractal dimension of cement particles and compression strength of cement mortars;
水泥颗粒粒度分布分形维与其胶砂抗压强度的关系研究
3) size distribution fractal


粒度分布分维数
1.
The influence of processing parameters on size distribution fractal possessed by FGH95 powders;
工艺参数对FGH95合金粉末粒度分布分维数的影响
4) fractal dimension of particle


粒度分形维数
5) diameter distributing fractal dimension


粒径分布分形维
1.
Purple soil aggregates and water-stable aggregates were analyzed by using geometric mean diameter (GMD), mean weight diameter (MWD), diameter distributing fractal dimension(D) and aggregate surface fractal di-mension(P) .
用团聚体几何平均直径(GMD)、平均重量直径(MWD)、粒径分布分形维(D)和表面分形维(P)分别对紫色土团聚体及水稳性团聚体进行分析:几何平均直径(GMD)、平均重量直径(MWD)、粒径分布分形维(D)和表面分形维(P)从不同角度反映紫色土团聚体特征;几何平均直径(GMD)、平均重量直径(MWD)对团聚体和水稳性团聚体分布均能较好地反映;粒径分布分形维(D)和表面分形维(P)能更好地反映团聚体的水稳性和抗蚀性,是描述土壤团聚体水稳性和抗蚀性的新指标和新方法。
6) particle size distribution fractal dimension


粒度分布分维
补充资料:分形维数
| 分形维数 fractal dimension 描述分形最主要的参量。简称分维。通常欧几里德几何中,直线或曲线是1维的,平面或球面是2维的,具有长、宽、高的形体是 3 维的;然而对于分形如海岸线、科赫曲线、射尔宾斯基海绵等的复杂性无法用维数等于 1、2、3 这样的数值来描述。科赫曲线第一次变换将1英尺的每边换成4个各长4英寸的线段,总长度变为 3×4/3=4 英尺;每一次变换使总长度变为乘以4/3,如此无限延续下去,曲线本身将是无限长的。这是一条连续的回线,永远不会自我相交,回线所围的面积是有限的,它小于一个外接圆的面积。因此科赫曲线以它无限长度挤在有限的面积之内,确实是占有空间的 ,它比1维要多,但不及2维图形,也就是说它的维数在1和2之间,维数是分数。同样,谢尔宾斯基海绵内部全是大大小小的空洞,表面积是无限大,而占有的 3 维空间是有限的,其维数在2和3之间。 计算分形维数的公式是 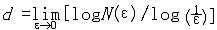 ,式中ε是小立方体一边的长度, N (ε)是用此小立方体覆盖被测形体所得的数目,维数公式意味着通过用边长为ε的小立方体覆盖被测形体来确定形体的维数。对于通常的规则物体 ,覆盖一根单位 长度的线 段所需 的数目要 N (ε)=1/ε2,覆盖一个单位边长的正方形,N(ε)=(1/ε)2 ,覆盖单位边 长的立方体,N (ε)=(1/ε)3。从这三个式子可见维数公式也适用于通常的维数含义。利用维数公式可算得科赫曲线的维数 d=1.2618,谢尔宾斯基海绵的维数d= 2.7268。对于无规分形,可用不同的近似方法予以计算,也可用一定的适当方法予以测定。 ,式中ε是小立方体一边的长度, N (ε)是用此小立方体覆盖被测形体所得的数目,维数公式意味着通过用边长为ε的小立方体覆盖被测形体来确定形体的维数。对于通常的规则物体 ,覆盖一根单位 长度的线 段所需 的数目要 N (ε)=1/ε2,覆盖一个单位边长的正方形,N(ε)=(1/ε)2 ,覆盖单位边 长的立方体,N (ε)=(1/ε)3。从这三个式子可见维数公式也适用于通常的维数含义。利用维数公式可算得科赫曲线的维数 d=1.2618,谢尔宾斯基海绵的维数d= 2.7268。对于无规分形,可用不同的近似方法予以计算,也可用一定的适当方法予以测定。分维反映了复杂形体占有空间的有效性,它是复杂形体不规则性的量度。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条