1) Elliptic junction line


椭圆相贯线
2) Column intersection line


圆柱相贯线
3) crossing curve of cylinder pipes


圆管相贯线
4) circular cones /intersecting curve/hyperbola/projection


圆锥/相贯线/双曲线/投影
5) phase el-lipse


相椭圆
6) correlation ellipse


相关椭圆
补充资料:画法几何:相贯线
相贯线
两空间形体表面的交线(见图 相贯线 )﹐是画法几何研究的一项内容。相贯线的形状取决於两立体的形状﹑大小和相对位置。如两空间形体的表面都是曲面﹐相贯线是一条空间曲线﹔两空间形体的表面都是平面时﹐相贯线是一条空间折线﹔两空间形体的表面分别是平面和曲面时﹐相贯线是由几段平面曲线围成的线。在给定两空间形体后﹐在多面正投影图中可以容易地画出两立体的投影﹐但它们的相贯线的投影并不能直接画出﹐通常採用辅助面法或其他方法先求出相贯线上若干点的投影﹐然后将它们连接成相贯线。辅助面法是先作出一适当的面﹐再作出该面和两空间形体的交线﹐最后作出两交线的交点。所得交点就是相贯线上的点。按此方法改变辅助面的位置﹐重复作图﹐就能得到足够的点﹐将它们连结成相贯线。图 相贯线
)﹐是画法几何研究的一项内容。相贯线的形状取决於两立体的形状﹑大小和相对位置。如两空间形体的表面都是曲面﹐相贯线是一条空间曲线﹔两空间形体的表面都是平面时﹐相贯线是一条空间折线﹔两空间形体的表面分别是平面和曲面时﹐相贯线是由几段平面曲线围成的线。在给定两空间形体后﹐在多面正投影图中可以容易地画出两立体的投影﹐但它们的相贯线的投影并不能直接画出﹐通常採用辅助面法或其他方法先求出相贯线上若干点的投影﹐然后将它们连接成相贯线。辅助面法是先作出一适当的面﹐再作出该面和两空间形体的交线﹐最后作出两交线的交点。所得交点就是相贯线上的点。按此方法改变辅助面的位置﹐重复作图﹐就能得到足够的点﹐将它们连结成相贯线。图 相贯线 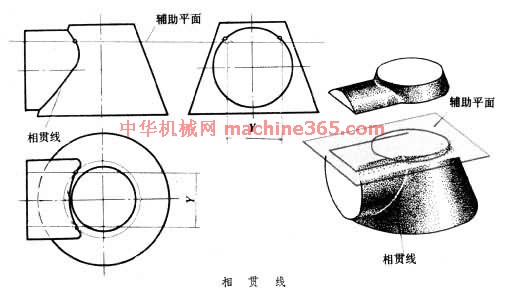 中为圆柱和圆锥台相交﹐为作出其相贯线上的点﹐选用水平面为辅助面﹐水平面与圆柱﹑圆锥台的交线分别是开口矩形和圆。它们的两个交点是相贯线上的点。运用辅助面法的关键在於选取合适的辅助面﹐辅助面和两空间形体表面的交线投影应是直线或者是圆。作图中常选用平面或球面为辅助面
中为圆柱和圆锥台相交﹐为作出其相贯线上的点﹐选用水平面为辅助面﹐水平面与圆柱﹑圆锥台的交线分别是开口矩形和圆。它们的两个交点是相贯线上的点。运用辅助面法的关键在於选取合适的辅助面﹐辅助面和两空间形体表面的交线投影应是直线或者是圆。作图中常选用平面或球面为辅助面
两空间形体表面的交线(见图 相贯线
 )﹐是画法几何研究的一项内容。相贯线的形状取决於两立体的形状﹑大小和相对位置。如两空间形体的表面都是曲面﹐相贯线是一条空间曲线﹔两空间形体的表面都是平面时﹐相贯线是一条空间折线﹔两空间形体的表面分别是平面和曲面时﹐相贯线是由几段平面曲线围成的线。在给定两空间形体后﹐在多面正投影图中可以容易地画出两立体的投影﹐但它们的相贯线的投影并不能直接画出﹐通常採用辅助面法或其他方法先求出相贯线上若干点的投影﹐然后将它们连接成相贯线。辅助面法是先作出一适当的面﹐再作出该面和两空间形体的交线﹐最后作出两交线的交点。所得交点就是相贯线上的点。按此方法改变辅助面的位置﹐重复作图﹐就能得到足够的点﹐将它们连结成相贯线。图 相贯线
)﹐是画法几何研究的一项内容。相贯线的形状取决於两立体的形状﹑大小和相对位置。如两空间形体的表面都是曲面﹐相贯线是一条空间曲线﹔两空间形体的表面都是平面时﹐相贯线是一条空间折线﹔两空间形体的表面分别是平面和曲面时﹐相贯线是由几段平面曲线围成的线。在给定两空间形体后﹐在多面正投影图中可以容易地画出两立体的投影﹐但它们的相贯线的投影并不能直接画出﹐通常採用辅助面法或其他方法先求出相贯线上若干点的投影﹐然后将它们连接成相贯线。辅助面法是先作出一适当的面﹐再作出该面和两空间形体的交线﹐最后作出两交线的交点。所得交点就是相贯线上的点。按此方法改变辅助面的位置﹐重复作图﹐就能得到足够的点﹐将它们连结成相贯线。图 相贯线  中为圆柱和圆锥台相交﹐为作出其相贯线上的点﹐选用水平面为辅助面﹐水平面与圆柱﹑圆锥台的交线分别是开口矩形和圆。它们的两个交点是相贯线上的点。运用辅助面法的关键在於选取合适的辅助面﹐辅助面和两空间形体表面的交线投影应是直线或者是圆。作图中常选用平面或球面为辅助面
中为圆柱和圆锥台相交﹐为作出其相贯线上的点﹐选用水平面为辅助面﹐水平面与圆柱﹑圆锥台的交线分别是开口矩形和圆。它们的两个交点是相贯线上的点。运用辅助面法的关键在於选取合适的辅助面﹐辅助面和两空间形体表面的交线投影应是直线或者是圆。作图中常选用平面或球面为辅助面
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条