1) Integral
[英]['ɪntɪɡrəl] [美]['ɪntəgrəl]


积分
1.
Indefinite integral of binary fractal interpolating function;


二元分形插值函数的不定积分
2.
A Nonlinear Servo Control Method Based on Integral Backstepping Scheme;


一种基于积分反推原理的非线性伺服控制方法
3.
A practical vector integral in three dimensions sphere shell;


三维球壳空间矢势积分的求解
2) integration
[英][,ɪntɪ'ɡreɪʃn] [美]['ɪntə'greʃən]


积分
1.
The integration of fractal interpolation surface function on various scales;


不同尺度下分形插值曲面函数的积分
2.
Maple 11 s Application in the Integration;


Maple11在积分中的应用
3) integrals
[英]['intigrəl] [美]['ɪntəgrəl]


积分
1.
The asymptote behavior of intermediate point in the Mean Value Theorem for integrals;


关于积分中值定理的中间值的渐进性质
2.
Symmetry's Application in Integrals


对称原理在积分计算中的应用
3.
Based on numerical integrals, the model parameters are estimated from the differential equation without iterations, the method is very effective in overcoming large amounts of measurement noise in the output.
提出一种简单但鲁棒性强的传感器动态建模方法,该方法基于数值积分思想,能有效克服测量噪声,无需迭代即可直接从微分方程辨识出模型参数,所建模型阶次较低、准确度较高,且较易实现递推算法,为传感器改善动态特性、实现动态补偿提供一种有效方法。
4) Integrate
[英]['ɪntɪɡreɪt] [美]['ɪntə'gret]


积分
1.
Application of integrate function of LabWindows/CVI5.


0积分函数在动态数据采集中的应用方法 ;直接应用积分函数对动态采集数据积分带来的问题及如何通过数据处理来实现数据积分 ;介绍一个程序实例。
5) integral calculus


积分
1.
Objective To develop the diagnosis value of electrophoresis scanning integral calculus of serum proteins in various kidney diseases.
目的 探讨REP高压快速蛋白电泳扫描积分对肾脏疾病的诊断和鉴别诊断价值。
2.
The writer gives the proof of rectangle area and derives integral calculus.


给出了矩形面积的证明,并由此推出了面积积分。
3.
Odd and even function’s integral calculation is a kind of particular operation in integral calculus,if the character of odd and even function can be applied flexibly in the process of calculating,it will play a role of simplifying calculation.
奇偶函数的积分计算是积分学中的一种特殊运算,在计算过程中如能巧用奇偶函数的性质,往往可以起到化难为易、简化计算的作用。
补充资料:积分
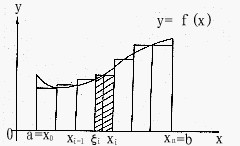
| 积分 integral 从不同的问题抽象出来的两个数学概念。定积分和不定积分的统称。不定积分是为解决求导和微分的逆运算而提出的。例如:已知定义在区间I上的函数f(x),求一条曲线y=F(x),x∈I,使得它在每一点的切线斜率为F′(x)= f(x)。函数f(x)的不定积分是f(x)的全体原函数(见原函数),记作 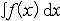 。如果F(x)是f(x)的一个原函数,则 。如果F(x)是f(x)的一个原函数,则 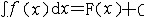 ,其中C为任意常数。例如, ,其中C为任意常数。例如,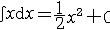 定积分是以平面图形的面积问题引出的。如右上图,y=f(x)为定义在[a,b]上的函数,为求由x=a,x=b ,y=0和y=f(x)所围图形的面积S,采用古希腊人的穷竭法,先在小范围内以直代曲,求出S的近似值,再取极限得到所求面积S,为此,先将[a,b]分成n等分:a=x0<x1<…<xn=b,取ζi∈[xi-1,xi],记Δxi=xi-xi-1, 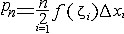 ,则pn为S的近似值,当n→+∞时,pn的极限应可作为面积S。把这一类问题的思想方法抽象出来,便得定积分的概念:对于定义在[a,b]上的函数y=f(x),作分划a=x0<x1<…<xn=b,若存在一个与分划及ζi∈[xi-1,xi]的取法都无关的常数I,使得 ,则pn为S的近似值,当n→+∞时,pn的极限应可作为面积S。把这一类问题的思想方法抽象出来,便得定积分的概念:对于定义在[a,b]上的函数y=f(x),作分划a=x0<x1<…<xn=b,若存在一个与分划及ζi∈[xi-1,xi]的取法都无关的常数I,使得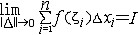 ,其中 ,其中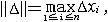 则称I为f(x)在[a,b]上的定积分,表为 则称I为f(x)在[a,b]上的定积分,表为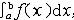 即 即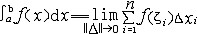 称[a,b]为积分区间,f(x)为被积函数,a,b分别称为积分的上限和下限。当f(x)的原函数存在时,定积分的计算可转化为求f(x)的不定积分: 称[a,b]为积分区间,f(x)为被积函数,a,b分别称为积分的上限和下限。当f(x)的原函数存在时,定积分的计算可转化为求f(x)的不定积分: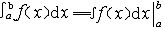 这是牛顿莱布尼兹公式。例如, 这是牛顿莱布尼兹公式。例如,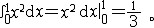
|
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条