1) functional
[英]['fʌŋkʃənl] [美]['fʌŋkʃənḷ]


泛函
1.
Functional Network Neurons Construct Theory and Method;


泛函网络神经元构造理论与方法
2.
Sufficient conditions of two integral type functional extrema;


两类积分型泛函极值问题的充分条件
3.
Proof on Frechet differentiability of functional;


关于泛函Fréchet可微性的证明
2) function
[英]['fʌŋkʃn] [美]['fʌŋkʃən]


泛函
1.
The extremum of function in mathematical physics;


数学物理问题中的泛函极值
2.
A function in the circular discontinuous wave-guide;


不连续圆形波导中的泛函
3.
The existence of almost periodic solution and stability for functional delay-differential equations with infinite delays;
具有无穷时滞泛函微分方程概周期解的存在性与稳定性
3) Liapunov Functional/function


Liapunov泛函/函数
4) Lyapunov function(functional)


Lyapunov函数(泛函)
5) density functional theory


密度泛函
1.
Comparative studies on the structures of porphyrin(H_2P),using hartree-fock and density functional theory methods;
卟吩结构的HARTREE-FORCK和密度泛函研究比较
2.
Study of density functional theory on N-alkylpyridium cations and aluminium chloride anions;
烷基吡啶及氯化铝正负离子结构的密度泛函研究
3.
The density functional theory study on the fluorescent emission spectra of naphthaline derivatives;
萘类衍生物荧光发射光谱的密度泛函理论研究
6) DFT


密度泛函
1.
DFT Study of Asymmetrical Annular-Addition of Methylenecyclopropanes with 1,3-Dicarbonyl Compound Free Radicals;
亚甲基环丙烷与1,3-双羰基化合物自由基不对称环加成反应的密度泛函研究
2.
DFT study on heterobinuclear Cu(Ⅱ)-Co(Ⅱ) complex of N,N′-bis(3-carboxyl salicyl aminal ethylene) oxalamide;
N,N′-双(3-羧基水杨醛叉缩胺乙基)草酰胺Cu(Ⅱ)-Co(Ⅱ)异双核配合物的密度泛函研究
3.
The Synthesis and DFT Research of Tetraethyl 1,2-Diphenylethane-1,1,2,2-Tetracarboxylate;


1,2-二苯基-1,1,2,2-四乙氧基羰基乙烷的合成及密度泛函计算研究
补充资料:泛函
| 泛函 functional 定义于一般集合,取数值(实数值或复数值)的映射。又称泛函数。是微积分中函数概念的发展和拓广。例如,取非空集X={f:f为定义在[a,b]上的连续函数},映射F:X→R为F(f)= 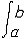 f(x)dx。F就是定义在集合X上的一个泛函。因此,泛函可通俗地看作以函数为自变元的函数,在很多情况下,泛函的定义域均为函数集。泛函概念的产生直接与变分法中的求极值问题有关。上面的例子还具有这样的性质: f(x)dx。F就是定义在集合X上的一个泛函。因此,泛函可通俗地看作以函数为自变元的函数,在很多情况下,泛函的定义域均为函数集。泛函概念的产生直接与变分法中的求极值问题有关。上面的例子还具有这样的性质: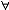 f,g∈X 和 f,g∈X 和 α,β∈R,有以下等式成立:F(αf+βg)= α,β∈R,有以下等式成立:F(αf+βg)= [αf(x)+βg(x)]dx= α [αf(x)+βg(x)]dx= α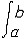 f(x)dx+β f(x)dx+β g(x)dx=αF(f)+βF(g),称这样的泛函为线性泛函。线性泛函是算子理论研究的主要对象之一,也是研究空间性质及结构的重要工具。因为利用线性连续泛函可导出对偶空间(由定义在X上的一切线性连续泛函组成的集合,并赋以自然的加法、数乘运算及范数)的概念,而空间X与其对偶空间 X*间的关系对于认识空间本身的性质和研究算子的性质都起着基础的作用。 g(x)dx=αF(f)+βF(g),称这样的泛函为线性泛函。线性泛函是算子理论研究的主要对象之一,也是研究空间性质及结构的重要工具。因为利用线性连续泛函可导出对偶空间(由定义在X上的一切线性连续泛函组成的集合,并赋以自然的加法、数乘运算及范数)的概念,而空间X与其对偶空间 X*间的关系对于认识空间本身的性质和研究算子的性质都起着基础的作用。除此之外,对应于多线性算子有多重线性泛函概念,例如在希尔伯特空间中,双线性泛函作为表示工具在处理问题时十分方便有效。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条