1) biarc


双圆弧
1.
The Normal Direction Error of the Approximation Plane Cubic Curve with Biarc;


平面三次曲线的双圆弧逼近的法向误差
2.
In the garment pattern design,the biarc segment is used to connect two given points while satisfying their tangent directions respectively.
在服装纸样设计中,寻找一曲线来连接两给定端点且满足两端点的切线方向,即构造曲线与两控制边相切时,使用双圆弧来连接。
2) bi-arc


双圆弧
1.
To improve the rate of soccer robot shooting goal,bi-arcs are used to solve the shooting problem with collision avoidance and appropriate position holding.
为了提高机器人足球比赛中的成功率,在分析了基本算法不足的基础上,利用能够满足任意端点及其斜率要求的双圆弧曲线来解决机器人小车到达目标点的位置,以及姿态运动过程中遇到障碍物能够保持最佳姿态的射门问题,并利用优化设计中的复合形法进行了运动路径寻优。
2.
In this paper bi-arcs are used to solve the path-planning problem of collision avoidance and holding appropriate position because they meet two end-point and two end-tangent conditions.
基于机器人小车到达定点常用Turn-Run-Turn方法及PID方法的不足,利用双圆弧具有满足任意端点及其斜率要求的特性,来解决机器人小车到达目标点位置和姿态的运动过程中遇到障碍物及保持最佳姿态的路径规划问题。
3.
A path planning strategy and a corresponding tracking control algorithm, both for given environment, are presented based on bi-arc path representation.
由于双圆弧具有满足任意端点及其斜率条件的特性 ,所以非常适合于移动机器人路径规划问题 。
4) double-arc method


双圆弧法
1.
Computerized numerical control programming system of cycloidal-pin gear based on double-arc method
基于双圆弧法的摆线针轮数控编程系统设计
5) biarc fitting


双圆弧拟合
1.
Building on mathematical theories of calculation geometric and function approaching method, circular-arc spline fitting and biarc fitting are gived for tabulated curve, circular-arc spline fitting is invariant in geometry , it is simple and accurate than other kinds of spline curve in calculation.
文章从计算几何、函数逼近论等数学理论出发,对列表曲线进行了圆弧样条拟合和双圆弧拟合。
6) double-circular-arc gear


双圆弧齿轮
1.
Finite element analysis of double-circular-arc gear based on precise model building;


精确建模的双圆弧齿轮有限元分析
2.
The model establishes the base for the 3D digital design,analysis of the finity unit,dummy manufacture of the double-circular-arc gear.
依据任意转角位置的双圆弧齿轮齿面数学模型,利用Pro/E得到了完整轮齿面的精确齿轮模型。
3.
The expression of the axis section profile of grinding wheel used to machine double-circular-arc gear is derived in detail.
本文详细地推导出加工双圆弧齿轮的砂轮截面廓形的计算表达式、并研制了通用的计算程序。
补充资料:传动:圆弧齿轮传动
齿廓为圆弧形的点嚙合齿轮传动。通常有两种嚙合形式﹕小齿轮为凸圆弧齿廓﹐大齿轮为凹圆弧齿廓﹐称单圆弧齿轮传动﹔大﹑小齿轮在各自的节圆以外部分都做成凸圆弧齿廓﹐在节圆以内的部分都做成凹圆弧齿廓﹐称双圆弧齿轮传动(图1 圆弧齿轮嚙合的两种形式 )。

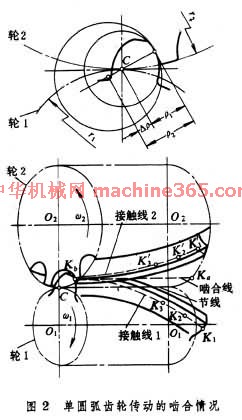
单圆弧齿轮传动 小齿轮的凸齿工作齿廓在节圆以外﹐齿廓圆心在节圆上﹔大齿轮的凹齿工作齿廓在节圆内﹐齿廓圆心略偏於节圆以外(图2 单圆弧齿轮传动的嚙合情况 )。由於大齿轮的齿廓圆弧半径p2 略大於小齿轮的齿廓半径p1﹐故当两齿廓转到K 点﹐其公法线通过节点c时﹐齿便接触﹐旋即分离﹐但与它相邻的另一端面的齿廓随即接触﹐即两轮齿K1﹑K'1﹐K2﹑K'2﹑K3﹑K'3 ……各点依次沿嚙合线接触。因此﹐圆弧齿轮任一端面上凹﹑凸齿廓仅作瞬时嚙合。一对新圆弧齿轮在理论上是瞬时点嚙合﹐故圆弧齿轮传动又常称为圆弧点嚙合齿轮传动。轮齿经过磨合后﹐实际上齿廓能沿齿高有相当长的一段线接触。圆弧齿轮传动的特点是﹕(1)综合曲率半径比渐开线齿轮传动大很多﹐其接触强度比渐开线齿轮传动约高0.5~1.5倍﹔(2)两轮齿沿嚙合线方向的滚动速度很大﹐齿面间易於形成油膜﹐传动效率较高﹐一般可达0.99~0.995﹔(3)圆弧齿轮沿齿高方向磨损均匀﹐且容易跑合﹔(4)圆弧齿轮无根切现象﹐故最小齿数可以少。但圆弧齿轮对中心距﹑切齿深度和螺旋角的误差敏感性很大﹐这三项误差对承载能力影响较大﹐故圆弧齿轮对製造和安装精度要求较高。此外﹐单圆弧齿轮轮齿弯曲强度较弱﹔切削同一模数的大﹑小齿轮﹐需用两把不同的滚刀。
双圆弧齿轮传动 工作时﹐从一个端面看﹐先是主动轮齿的凹部推动从动轮齿的凸部﹐离开后﹐再以它的凸部推动对方的凹部(图3 双圆弧齿轮传动的嚙合情况 )﹐故双圆弧齿轮传动在理论上同时有两个接触点﹐经跑合后﹐这种传动实际上有两条接触线﹐因此可以实现多对齿和多点嚙合。此外﹐由於其齿根厚度较大﹐双圆弧齿轮传动不仅承载能力比单圆弧齿轮传动约高30%以上﹐而且传动较平稳﹐振动和噪声较小﹐并且可用同一把滚刀加工相配对的两个齿轮。因此﹐高速重载时﹐双圆弧齿轮传动有取代单圆弧齿轮传动的趋向。

单圆弧齿轮传动 小齿轮的凸齿工作齿廓在节圆以外﹐齿廓圆心在节圆上﹔大齿轮的凹齿工作齿廓在节圆内﹐齿廓圆心略偏於节圆以外(图2 单圆弧齿轮传动的嚙合情况 )。由於大齿轮的齿廓圆弧半径p2 略大於小齿轮的齿廓半径p1﹐故当两齿廓转到K 点﹐其公法线通过节点c时﹐齿便接触﹐旋即分离﹐但与它相邻的另一端面的齿廓随即接触﹐即两轮齿K1﹑K'1﹐K2﹑K'2﹑K3﹑K'3 ……各点依次沿嚙合线接触。因此﹐圆弧齿轮任一端面上凹﹑凸齿廓仅作瞬时嚙合。一对新圆弧齿轮在理论上是瞬时点嚙合﹐故圆弧齿轮传动又常称为圆弧点嚙合齿轮传动。轮齿经过磨合后﹐实际上齿廓能沿齿高有相当长的一段线接触。圆弧齿轮传动的特点是﹕(1)综合曲率半径比渐开线齿轮传动大很多﹐其接触强度比渐开线齿轮传动约高0.5~1.5倍﹔(2)两轮齿沿嚙合线方向的滚动速度很大﹐齿面间易於形成油膜﹐传动效率较高﹐一般可达0.99~0.995﹔(3)圆弧齿轮沿齿高方向磨损均匀﹐且容易跑合﹔(4)圆弧齿轮无根切现象﹐故最小齿数可以少。但圆弧齿轮对中心距﹑切齿深度和螺旋角的误差敏感性很大﹐这三项误差对承载能力影响较大﹐故圆弧齿轮对製造和安装精度要求较高。此外﹐单圆弧齿轮轮齿弯曲强度较弱﹔切削同一模数的大﹑小齿轮﹐需用两把不同的滚刀。

双圆弧齿轮传动 工作时﹐从一个端面看﹐先是主动轮齿的凹部推动从动轮齿的凸部﹐离开后﹐再以它的凸部推动对方的凹部(图3 双圆弧齿轮传动的嚙合情况 )﹐故双圆弧齿轮传动在理论上同时有两个接触点﹐经跑合后﹐这种传动实际上有两条接触线﹐因此可以实现多对齿和多点嚙合。此外﹐由於其齿根厚度较大﹐双圆弧齿轮传动不仅承载能力比单圆弧齿轮传动约高30%以上﹐而且传动较平稳﹐振动和噪声较小﹐并且可用同一把滚刀加工相配对的两个齿轮。因此﹐高速重载时﹐双圆弧齿轮传动有取代单圆弧齿轮传动的趋向。
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条