1) Quantile dimension


分位量纲
2) dimensional analysis


量纲分析
1.
Experimental study on rapeseed extrusion cooking using dimensional analysis;


基于量纲分析的油菜籽挤压膨化试验参数的研究
2.
Research on Al_2O_3 ceramic membrane flux equation based on dimensional analysis;


基于量纲分析的氧化铝陶瓷膜通量关联式的研究
3.
Application of Linear Algebra in Dimensional Analysis;


线性代数在量纲分析中的应用
3) dimension analysis


量纲分析
1.
An analytical coupled water-energy balance equation at arbitrary time acale was derived by dimension analysis and mathematical derivation.
本文通过量纲分析和数学推导得到能用于任意时间尺度上的水热耦合平衡方程,该方程含有唯一参数。
2.
Then the method of dimension analysis is introduced,and a synthesis parameter composed by roo.
引入量纲分析的方法,构造了一个由空气温度、服装热阻和人体新陈代谢率综合作用的参数,并证明其合理性,并提出修正方案。
3.
We can deduce some physical laws through dimension analysis,which may provide theoretical instructions on scientifically organizing experimental processes and integrating experimental results.
量纲是物理学中的重要概念,量纲分析法在物理学中有重要的应用。
4) normalized displacements


无量纲位移
1.
The concepts of normalized displacements and transmissibility index are introduced.


引入无量纲位移和透射系数等概念,绘制了不同壁厚的刚性空心管桩屏障后的无量纲位移等值线、透射系数随管桩间距的变化曲线以及不同数量的管桩组成的屏障后的无量纲位移变化曲线等图件,通过进一步的分析得出单排非连续刚性空心管桩屏障的隔振效果随着管桩间距和壁厚的减小而提高、最佳隔离区域随着管桩数量的增多而增大等重要结论,为非连续刚性屏障的隔振设计提供了理论依据。
5) dimensionsless unit


无量纲单位
6) dimensionless analysis


无量纲分析
1.
Dimensionless analysis of thermodynamics parameters of free-piston Stirling cooler;


自由活塞型斯特林制冷机热力学参数的无量纲分析
补充资料:量纲分析
| 量纲分析 dimensional analysis 自然科学中一种研究和分析方法。它根据一切量所必须具有的形式来分析判断事物间数量关系所遵循的一般规律。通过量纲分析可以检查反映物理现象规律的方程在计量方面是否正确,甚至可提供寻找物理现象某些规律的线索。 人们通过定义各种物理量来描述物理现象,确定物理系统所处的状态。任一物理量的定义给出被定义量同有关量之间的关系。物理量之间的有规律联系还通过自然界的各种定律表示出来。因此当一个单位制的基本量确定后,其他量就可通过既定的关系或定律,定义为用基本量表示的导出量,并通过代数式表示为基本量的幂次乘积。例如力学中常用的MKS和CGS单位制,基本量都是长度L、质量M和时间T,而速度、加速度和力就是分别通过它们的定义和牛顿运动定律定义出来的导出量。国际单位制(SI)有7个基本量:长度L、质量M、时间T、电流I、温度 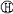 、物质的量N和发光强度J。 、物质的量N和发光强度J。量纲 各种物理量之间存在着关系,说明它们的结构必然由若干统一的基础成分组成,并按各成分的多寡形成量与量间的千差万别。物理量的这种基本构成成分统称为量纲。上面给出的L、M、T、I、 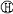 、N、J就分别是SI中7 个基本量的量纲。任一物理量Q的量纲可以表示为一组基本量的量纲的幂次积,即 、N、J就分别是SI中7 个基本量的量纲。任一物理量Q的量纲可以表示为一组基本量的量纲的幂次积,即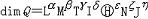 ,幂次指数a、β、γ、δ、ε、ζ、 ,幂次指数a、β、γ、δ、ε、ζ、 称为量纲指数。表中列出写成上面形式的一些物理量的量纲,其中1表示无量纲,即其量纲积内基本量的量纲指数均为零。由于选取的基本量不同,同一个物理量在不同单位制里的量纲可以不同。例如高斯单位制中的基本量是长度、质量和时间,电量q的量纲为L3/2M1/2T-1;而在电磁学的MKSA制中的基本量是长度、质量、时间和电流,所以电量的量纲为IT。无量纲量的量纲为1,其数值与所选用的单位制无关,用纯数表示。 称为量纲指数。表中列出写成上面形式的一些物理量的量纲,其中1表示无量纲,即其量纲积内基本量的量纲指数均为零。由于选取的基本量不同,同一个物理量在不同单位制里的量纲可以不同。例如高斯单位制中的基本量是长度、质量和时间,电量q的量纲为L3/2M1/2T-1;而在电磁学的MKSA制中的基本量是长度、质量、时间和电流,所以电量的量纲为IT。无量纲量的量纲为1,其数值与所选用的单位制无关,用纯数表示。
实际现象中总是同时参有许多物理量,它们之间通过理论和实验建立起一定的依存关系,构成某一客观规律的数学关系式。这个关系式必须在单位尺度的主观任意变换下不受破坏,这一性质称为关系式的“完整性”。保证多项式关系的完整性有两种办法:①要求出现在算式中的一切参量都是无量纲纯数。②要求式中所有各项具有完全相同的量纲,也就是每一项的每一基本量纲都有相同的幂次,即所谓量纲的齐次性。 基本定理 即π定理。根据量纲分析的原理寻求和简化物理量之间函数关系的定理。可表述为:若有一个量纲齐次性的方程,其中包含由m个独立的基本量所定义的n个物理量,则此方程必可演化为一个包含有(n-m)个独立的无量纲乘积的关系式。这就是说,如有一个包含n个变量q1,q2,…,qn的量纲齐次性的方程为F(q1,q2,…,qn)=0,则必可得一个包含k=n-m个独立的无量纲积的关系式f(π1,π2…,πk)=0。 以竖直下抛落体下降的距离公式 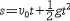 为例,式中u 0为初速,g为重力加速度,t为时间。根据π定理,上式可演化为一个包含有两个独立的无量纲积(u 0t/s)和(gt2/s)的关系式: 为例,式中u 0为初速,g为重力加速度,t为时间。根据π定理,上式可演化为一个包含有两个独立的无量纲积(u 0t/s)和(gt2/s)的关系式: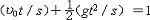 。这两个无量纲积是独立的,因为它们中的一个不能由另一个导出;由s、u 0、g、t组成的其他无量纲积都可由这两个无量纲积导出。在量纲分析中把具有这种性质的一组无量纲积称为完全系。 。这两个无量纲积是独立的,因为它们中的一个不能由另一个导出;由s、u 0、g、t组成的其他无量纲积都可由这两个无量纲积导出。在量纲分析中把具有这种性质的一组无量纲积称为完全系。应用 以单摆振动为例,说明量纲分析的应用。根据常识判断,描述单摆振动规律的运动方程中应包含以下物理量:周期t,摆长l,重力加速度g和摆角  。所以可将该方程粗略地写为F(t,l,g, 。所以可将该方程粗略地写为F(t,l,g, )=0。根据π定理,因k=n-m=4-2=2,所以应有两个独立的无量纲积:π1=gt2/l,π2= )=0。根据π定理,因k=n-m=4-2=2,所以应有两个独立的无量纲积:π1=gt2/l,π2= 。相应的无量纲关系式为f(gt2/l, 。相应的无量纲关系式为f(gt2/l, )=0,可改写为gt2/l= )=0,可改写为gt2/l=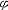 ( ( )或t=(l/g)1/2 )或t=(l/g)1/2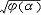 ,从而得到以下结论:当摆角 ,从而得到以下结论:当摆角 一定时,振动周期与摆长的平方根成正比。若只讨论小 一定时,振动周期与摆长的平方根成正比。若只讨论小 角的情况 ,则 角的情况 ,则 不再是重要的变量,可以不去考虑。由3个量l、g和t只能组成一个无量纲积t2g/l,故得t2g/l=常数= 不再是重要的变量,可以不去考虑。由3个量l、g和t只能组成一个无量纲积t2g/l,故得t2g/l=常数= 或t= 或t= (l/g)1/2。这就是说,简单的量纲分析可以导致一个正确的常数乘因子的解。 (l/g)1/2。这就是说,简单的量纲分析可以导致一个正确的常数乘因子的解。应用量纲分析于单摆振动的例子表明,从研究一个过程中各物理量的量纲及其间的关系,可以推导出必须加于这些物理量的某些限制,这是量纲分析的主要作用。这种方法既普遍又简单,但不能给出完全确定的解。在一些较为复杂包含很多物理量的过程中,有的不能从数学上严格求解,有的甚至列不出确切描述这一过程的方程。量纲分析得出的变量之间必须遵守的关系式,可以减少问题的不确定因素。在此基础上,应用相似理论,通过模型试验,确定关系式的一般函数形式,有很大的实际意义。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条