1) φ-variation


φ-变差
1.
By using probabilistic methods,the rate of convergence in terms of function f∈C(R)∩L∞(R)and the convergence rate in φ-variation function for the Gauss-Weierstrass operators were obtained.
利用概率方法研究了Gauss-Weierstrass算子关于函数f∈C(R)∩L∞(R)的逼近度,并利用这一逼近度进一步讨论了Gauss-Weierstrass算子在φ-变差函数下的收敛速度。
2) φ-bounded variation


φ-有界变差
1.
The main aim of this dissertation is to investigate estimates of Lp modulus of continuity w(f; t)_p (1 ≤ p < ∞) of the class of functions of Λφ-bounded variation and its special cases.
本文主要研究Λφ-有界变差函数类ΛφBV及其重要特殊情形的Lp连续模ω(f;t)_p(1≤p<∞)的估计问题。
3) bounded Φ-variation solutions


Φ有界变差解
1.
The existence theorem for bounded Φ-variation solutions to the Caratheodory system is established by using the bounded Φ-variation function theory, which was introduced by Musielak and Orlicz.
本文借助Musielak及Orlicz等人提出的Φ有界变差函数理论,建立了Caratheodory系统在Henstock-Kurzweil积分意义下的Φ有界变差解的存在性定理。
2.
In this paper,we discuss the bounded Φ-variation solutions of the Caratheodory system by combining the theories of function of bounded Φ-variation and the Caratheodory system.
本文将Φ有界变差函数理论与Caratheodory系统结合起来,讨论了Caratheodory系统的Φ有界变差解。
4) bounded Φ-variation solution


Φ-有界变差解
1.
Bounded Φ-Variation Solutions of Kurzweil Equations;


Kurzweil方程的Φ-有界变差解
2.
The local existence theorem of bounded Φ-variation solutions for impulsive differential equations at fixed times is established.
讨论了固定时刻脉冲微分系统与Kurzweil广义常微分方程之间的关系,建立了固定时刻脉冲微分系统Φ-有界变差解的局部存在性定理。
3.
In this paper, the bounded Φ-variation function and the generalized ordinary differen- tial equation are unified, the concept of Φ-variational stability is established and the stability of the bounded Φ-variation solutions to Kurzweil equations is discussed.
本文将Φ-有界变差函数理论与Kurzweil方程理论结合起来,首次给出了Φ-变差稳定性概念,讨论了Kurzweil方程Φ-有界变差解的稳定性,建立了Φ-界变差解Φ-变差稳定性和渐近Φ-变差稳定性的Ljapunov型定理。
5) function of Φ-bounded variation


Φ-有界变差函数
6) function of c-bounded variation


Φ有界变差函数
补充资料:有界变差函数
| 有界变差函数 bounded variation,function of 定义在区间[a,b]上,并能表为两个单调增函数之差的实值函数。属常用的函数类,它有许多好的性质,例如:有界变差函数必为有界函数;两个有界变差函数的和、差、积仍为有界变差函数;有界变差函数在[a,b]上黎曼可积;有界变差函数在[a,b]上几乎处处可导,导函数在[a,b]上勒贝格可积。此外还有,平面上由y=f(x)表示的曲线C可求长的充分必要条件是f为有界变差函数。应注意的是,连续函数不一定为有界变差函数。例如: 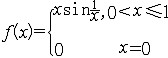 。 。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条