|
|
|
说明:双击或选中下面任意单词,将显示该词的音标、读音、翻译等;选中中文或多个词,将显示翻译。
|
|
|
1) rectangular plates with middle thickness

矩形中厚板
1.
Bending of rectangular plates with middle thickness, is transferred into Hamiltonian system.
从矩形中厚板弯曲问题的基本方程出发,将问题导入Hamilton体系,然后利用辛几何中的分离变量和本征函数展开的方法求出了矩形中厚板典型弯曲问题的解析解。
2) rectangular moderate thickness plate

中厚矩形板
1.
Nonlinear free vibration analysis including coupled effect of elastic foundation for rectangular moderate thickness plate with discontinuities;
弹性地基上间断中厚矩形板的非线性振动
3) moderate thickness rectangular plates

中厚矩形板
1.
Based on the theory of isotropic moderate thickness plates and using Hamilton variation principle, the nonlinear equations of motion including the nonlinear effect of plates and the coupled effect of foundation were derived for the moderate thickness rectangular plates on two parameter foundation.
基于各向同性中厚板理论,考虑板的非线性效应和地基耦合效应,应用Hamilton变分原理,建立了双参数地基上周边自由中厚矩形板的非线性运动控制方程,提出了一组满足问题全部边界条件的试函数。
4) Reissner rectangular moderately thick plate

Reissner矩形中厚板
5) thick rectangular plate

厚矩形板
1.
Bending of thick rectangular plates with adjacent simply supported andtwo-fixed edges under hydrostatic pressure;
复杂边界厚矩形板在静水压力作用下的弯曲
2.
Using RTM to solve the bending of thick rectangular plates with complex boundaries;

功的互等法解复杂边界条件下厚矩形板的弯曲
3.
Bending of thick rectangular plates with adjacent simply supported,one fixed and one free edges under hydrostatic pressure
静水压力作用下复合边界条件厚矩形板的弯曲
6) rectangular thick plate

矩形厚板
1.
The natural vibration of rectangular thick plate with double side multi-support is studied by using Laplace Transformation The characteristic equation of frequency and mode of vibration function are derivate
采用Laplace变换研究了两对边简支多支承矩形厚板的固有横振,并给出了其振型函数及频率的特征方程。
2.
We get the exact solution of rectangular thick plates with two adjacent flee edges and two arbitrary edges.
选取由三角级数和多项式组成的挠度函数w(x,y)和应力函数Ψ(x,y),得到相邻边自由另两边任意支承矩形厚板的精确解、它不需要繁琐地叠加。
补充资料:矩形
一.型态分析 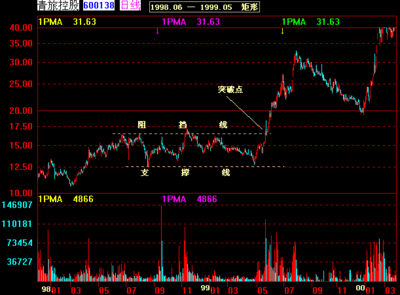
矩形是股价由一连串在二条水平的上下界线之间变动而成的型态。股价在其范围之内出现上落。价格上升到某水平时遇上阻力,掉头回落,但很快地便获得支持而升,可是回升到上次同一高点时再一次受阻,而挫落到上次低点时则再得到支持。这些短期高点和低点分别以直线连接起来,便可以绘出一条通道,这通道既非上倾,亦非下降,而是平行发展,这就是矩形型态。 [编辑] 二.市场含义 矩形为冲突型,是描述实力相当的争战双方的竞争。 这型态明显告诉我们,好淡双方的力量在该范围之间完全达致均衡状态,在这段期间谁占不了谁的便宜。看好的一方认为其价位是很理想的买入点,于是股价每回落到该水平即买入,形成了一条水平的需求线。与此同时,另一批看淡的投资者对股市没有信心,认为股价难以升越其水平,于是股价回升至该价位水平,便即沽售,形成一条平行的供给线。从另一个角度分析,矩形也可能是投资者因后市发展不明朗,投资态度变得迷惘和不知所措而造成。所以,当股价回升时,一批对后市缺乏信心的投资者退出;而当股价回落时,一批憧憬着未来前景的投资者加进,由于双方实力相若,于是股价就来回在这一段区域内波动。 一般来说,矩形是整理形态,市道牛皮上落,顺升市和跌市中都可能出现,长而窄且成交量小的矩形在原始底部比较常出现。突破上下了限后有买入和卖出的讯号,涨跌幅度通常等于矩形本身宽度。 [编辑] 三.要点提示 (1)矩形形成的过程中,除非有突发性的消息扰乱,其成交量应该是不断减少的。如果在型态形成期间,有不规则的高成交出现,型态可能失败。当股价突破矩形上限的水平时,必须有成交量激增的配合;但若跌破下限水平时,就不须高成交量的增加。 (2)矩形呈现突破后,股价经常出现反抽,这种情形通常会在突破后的三天至三星期内出现。反抽将止于顶线水平之上,往下跌破后的假性回升,将受阻于底线水平之下。 (3)一个高,低波幅较大的矩形,较一个狭窄而长的矩形型态更具威力。
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|






