1) three-valued logic metric space
三值逻辑度量空间
1.
Let(F(S),ρ3) be the three-valued logic metric space.
对三值命题逻辑系统L_3~*中逻辑理论的相容性、全发散性以及逻辑闭性给出了它们在三值逻辑度量空间(F(S),ρ_3)中的拓扑刻画。
2) logical metric space
逻辑度量空间
1.
And the structures of the four logical metric spaces induced by corresponding logical metric are studied,and get some good results.
在4种逻辑代数中分别建立了逻辑度量,讨论了其性质,并对它们之间的关系进行了详尽地讨论;又对4个逻辑度量空间的结构及其性质进行了详细地讨论,并得到一些好的结果。
2.
As an application,the distance between a formula and a Γ-conclusion set and the different Γ-conclusion set of logical metric space(F(S),ρ) is described.
作为应用,给出了逻辑度量空间(F(S),ρ)中一个公式到一个Γ推论之集以及不同Γ推论之集间的距离描述。
3.
And the structure and property of the logical metric space are studied and some good results have been obtained.
给出了乘积代数的定义,讨论了其性质,并建立了乘积代数的度量,对逻辑度量空间的结构及其性质进行了讨论,得到了一些好的结果。
3) D-logic Metric Space
D-逻辑度量空间
1.
The Theory of Consistency Degree in D-logic Metric Space
D-逻辑度量空间中的相容理论
2.
It is proved that the set of values of D-randomized truth degree of formulas has no isolated point in[0,1];The concepts of D-logic pseudo-metric and D-logic metric space are also introduced.
通过随机化赋值集的方法,在二值逻辑中提出了公式的D-随机真度概念,证明了全体公式的D-随机真度之集在[0,1]中没有孤立点;提出了D-逻辑伪距离和D-逻辑度量空间,证明了该空间中没有孤立点;指出当取均匀概率测度,且各概率测度均为1/2时,D-随机真度就转化为计量逻辑学中的真度,同时两公式间的D-逻辑伪距离就转化为计量逻辑学中的伪距离,从而建立了更具一般性的随机逻辑度量空间;最后在D-逻辑度量空间中提出了3种不同类型的近似推理模式,并证明了这三种模式是等价的。
3.
A series of D-logic pseudo metric inequalities related to the finite theory in D-logic metric space are then obtained.
以D-随机真度为基础,给出了公式到有限理论结论集D-逻辑伪距离的D-随机真度表示式,得到了D-逻辑度量空间中与有限理论相关的一系列D-逻辑伪距离不等式,并在D-逻辑度量空间中进行了近似推理讨论。
4) DG3-logic metric space
DG3-逻辑度量空间
1.
DG3-logic metric space was built.
利用赋值集的随机化方法,在三值逻辑G3中提出了公式的随机真度,证明了所有公式的随机真度之集在[0,1]中没有孤立点;给出了两公式间的DG3-相似度与伪距离的概念,并建立了DG3-逻辑度量空间,证明了此空间没有孤立点。
5) Logic Metric Space
逻辑度量空间
1.
The degree of variation functionρ between two formulas are introduced using eontrodiction de- gree,and it is proved to be a pseduo-metrie,then logic metric space (F(S),ρ ) are built.
用矛盾度定义了公式之间的差异度函数ρ',证明了ρ'是一个伪度量,从而在F(S)上建立了逻辑度量空间(F(S),ρ')。
2.
The degree of variation function ρ between two formulas are introduced using controdiction degree,and it is proven to be a pseduo-metric,then logic metric space(F(S),ρ ) are built.
将n值R0-命题逻辑系统Ln*中的矛盾式概念程度化,引入了矛盾度的概念,并且讨论了公式的矛盾度的若干重要性质,进而用矛盾度定义了公式之间的差异度函数ρ',证明了ρ'是一个伪度量,从而在F(S)上建立了逻辑度量空间(F(S),ρ')。
3.
Let (F(S),ρ) be the logic metric space of two-valued propositional logic.
在二值命题逻辑系统中基于逻辑度量空间(F(S),ρ)而建立起了逻辑理论的发散性、相容性和理论的拓扑性质之间的联系。
6) DW3-logic Metric Space
DW3-逻辑度量空间
补充资料：度量空间
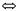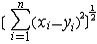| 度量空间 metric space 具有度量的抽象空间，设X是一个集合，若有定义在X×X上的非负实值函数d，满足①d（x，y）≥0，d（x，y）＝0  x＝y； ②d（x，y）＝d（y，x）；③d（x，z）≤d（x，y）＋d（y，z），则称（X，d）是度量空间，d称为距离或度量。这是最接近于欧几里得空间的抽象空间。利用度量可很自然地将欧几里得空间上点的邻域、开集、闭集，收敛序列以及连续映射等概念推广到一般度量空间，也能将一致连续的概念推广到度量空间。由于19世纪末集合论产生后，实变函数及泛函分析的发展，需要规定函数间的距离，因而抽象出度量、度量空间的概念，其创始人是M.R.弗雷歇。常见的度量空间有：n维欧几里得空间（Rn,d）：Rn＝｛（x1，…，xn）｜xi∈R，i＝1，2，…，n ｝，d（x，y）＝  ，其中x＝（x1，x2，…， xn），y＝（y1，y2，…，yn）。希尔 伯特空 间（l2；d）：l2＝｛（x1，x2，…，xn…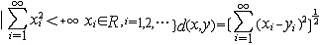）  ， 其中x ＝( x1，x2 ，…），y＝（y1，y2，…）∈l2。函数空间(ρ[0，1］，d)：C[0，1］＝｛f：f为[0，1］上的实值连续函数｝，对任意f，g∈C[0，1］，d(f，g)＝max｛｜f（x）－g（x）｜｝。 x∈[0，1］ 对度量空间（X，d）可引进拓扑结构，即以包含开球B（x，r）＝｛y∈X｜d（ x，y）＜r ｝的集为邻域定义拓扑，称为d所诱导的拓扑。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条