1) Least square ellipse fitting
最小二乘椭圆拟合
2) lease-square method for ellipse fitting
最小二乘法拟合椭圆
4) least square ellipse
最小二乘椭圆
1.
It describes that fitting laser spot to obtain 5 independent parameters based on the principle of least square ellipse and establishing the relationship between spatial plane and elliptical parameters.
由最小二乘椭圆拟合法得到椭圆光斑的5个独立参数,并建立空间平面与椭圆参数之间的关系,采用SWIFT算法进行搜索求解,无需特征点匹配,即可确定空间平面的位姿。
5) least square arc fitting
最小二乘法圆弧拟合
6) Least squares analysis
最小二乘法拟合圆
补充资料：最小二乘法
| 最小二乘法 least square，method of 科学实验和统计工作中常用的一种数据处理方法。由A.M.勒让德和C.F.高斯于19世纪初分别独立提出。例如要从一组实验数据（xi，yi）（i=1，2，…，m）中，寻找自变量x与因变量y之间的函数关系y=F（x）。由于观测数据往往不准确，因率不要求y=F（x）经过所有数据点，而只要求所在所有给定点xi上的偏差ri＝F（xi）－yi（i＝1，2，…，m）的平方和 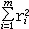 达到最小。F（x）的函数类型往往与实验的物理背景以及数据的实际分布有关，它一般含有某些待定参数。如果F（x）是所有待定参数的线性函数，那么相应的问题称为线性最小二乘问题，否则称为非线性最小二乘问题。最小二乘法还是实验数据参数估计的重要工具。这是因为这种方法比其他方法更容易理解，即使在其他方法失效的情况下，用最小二乘法还能提供解答，而且从统计学的观点分析，用该方法求得各项估计具有最优统计特征，因此这一方法也是系统识别的重要基础。线性最小二乘问题可以借助多元微分学知识通过求解法方程组得到解答。求解非线性最小二乘问题比较困难，一般要用线性化方法或最优化方法才行。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条