1) culminating adj.


达绝顶的;终极的;最后的
2) ultimate
[英]['ʌltɪmət] [美]['ʌltəmət]


极限,顶点,最后的,主要的
3) Ultimate
[英]['ʌltɪmət] [美]['ʌltəmət]


最终的,最后的
4) ultimate
[英]['ʌltɪmət] [美]['ʌltəmət]


极限的,最大的;根本的,基本的;最后的,最终的
5) ult.


最终的;极限的
6) ultimate
[英]['ʌltɪmət] [美]['ʌltəmət]


最后的,最终的;根本的
补充资料:极限
| 极限 limit 微积分学乃至分析数学的基本概念之一,用于描述变量在某一变化过程中的变化趋势。极限的朴素思想和应用可追溯到古代,中国早在2000年前就已能算出方形、圆形、圆柱等几何图形的面积和体积,3 世纪刘徽创立的割圆术,就是用圆内接正多边形面积的极限是圆面积这一思想来近似计算圆周率π的。并指出“割之弥细,所失弥少,割之又割,以至不可割,则与圆合体而无所失矣”。随着微积分学的产生,极限概念被明确提出,但含糊不清,直至19世纪,由A.-L.柯西、K.魏尔斯特拉斯等人的工作 ,以及实数理论的建立,才使极限理论建立在严密的理论基础之上。 对于给定的数列 an,如果当n无限增大时,an 有确定的变化趋势棗与某一实数a无限接近,则说数列 an以a为极限,记作 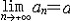 。例如,数列 。例如,数列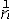 以0为极限,即 以0为极限,即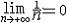 ,又如 ,又如 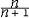 的极限为1,即 的极限为1,即 。数列极限有以下四则运算法则:设 。数列极限有以下四则运算法则:设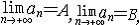 则有 则有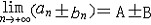 , ,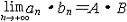 , , 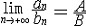 (B≠0)。任给一个数列 an,不一定有极限,例如,1,-1,1,-1,…和2,4,6,…,2n,…,但后一个数列当n无限增大时,an=2n也无限增大,此时也说an趋于正无穷大,记作 (B≠0)。任给一个数列 an,不一定有极限,例如,1,-1,1,-1,…和2,4,6,…,2n,…,但后一个数列当n无限增大时,an=2n也无限增大,此时也说an趋于正无穷大,记作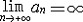 。 。对于给定的函数y=f(x),如果在x=x0点附近有定义(在x0点可以没有定义),并且当x无限接近x时,f(x)与某一实数A无限接近,则称A为f(x)当x趋向于x0时的极限,记作 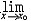 f(x)=A。例如f(x)=x2当x→ f(x)=A。例如f(x)=x2当x→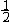 的极限为 的极限为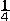 ,又如 ,又如 。函数极限也有以下四则运算法则:设 。函数极限也有以下四则运算法则:设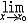 f(x)=A, f(x)=A,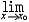 g(x)=B,则有[f(x)±g()]=A±B,f(x)·g(x)=A·B, g(x)=B,则有[f(x)±g()]=A±B,f(x)·g(x)=A·B,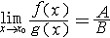 (B≠0)。 (B≠0)。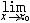 f(x)=A表示当 x无限增大时,f(x)与实数A无限接近,即f(x)以A为极限。 f(x)=A表示当 x无限增大时,f(x)与实数A无限接近,即f(x)以A为极限。函数极限与数列极限有以下关系: 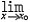 f(x)=A,当且仅当对每一以x0为极限的数列xn,有f(xn)→A(xn≠ x0)。这可以将函数的极限问题转化为数列极限问题来考虑。在某些情况下,是非常有效的。例如,从 f(x)=A,当且仅当对每一以x0为极限的数列xn,有f(xn)→A(xn≠ x0)。这可以将函数的极限问题转化为数列极限问题来考虑。在某些情况下,是非常有效的。例如,从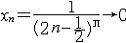 , ,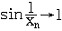 和 和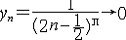 , , ,可知当 x→0时 , ,可知当 x→0时 ,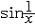 没有极限。 没有极限。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条