






研究不确定性决策问题的一种系统分析方法。其目的是改进决策过程﹐从一系列备选方案中找出一个能满足一定目标的合适方案。决策分析有四个基本要素﹕方案﹑结局(有时也称后果)﹑效用和偏好。
发展简况 早在1738年﹐伯努利就已提出决策分析中的效用概念。从1763年贝叶斯发表条件概率起就出现统计推断理论的萌芽。1815年拉普拉斯又将它推向一个新的阶段。统计推断理论实际上是在风险情况下的决策理论。1931年﹐拉姆齐基於效用和主观概率两个基本概念来研究决策理论。1944年 诺伊曼﹐J.von和O.莫根施特恩在著名的《竞赛理论与经济行为》一书中﹐独立地研究了在不确定情况下进行决策所用的近代效用理论。沃尔德在1950年提出的统计决策函数是决策理论的又一重要进展。1954年萨维奇为决策方法提供了公理系统和严格的哲学基础。60年代初期﹐美国哈佛商学院开始运用统计决策理论解决商业问题﹐并定名为应用统计决策理论。1966年﹐美国霍华德首先应用决策分析这个名词。后来﹐决策分析又有许多新的发展﹐并广泛吸取有关的决策方法﹐从而形成一个内容广泛﹑实用性很强的学科分支。现代决策分析的发展动向是研究人们决策的行为思想方面和研製与计算机结合的决策支持系统等。
决策步骤 决策分析一般分 4个步骤(见图 决策步骤关係图 )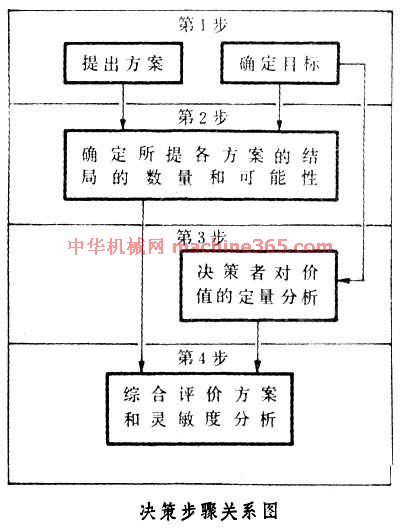 ﹕形成决策问题﹐包括提出方案和确定目标及其效果量度。用概率来定量地描述每个方案所產生的各种结局的可能性。决策者对各种结局的价值定量化﹐一般用效用来表示﹐效用可用效用值来定量。效用值是各决策人根据个人的意志和经验及其所处环境条件等因素﹐对各种结局的价值所作的定量估计。有了效用就能给出偏好。综合分析和评价各方面信息﹐以最后决定方案的取捨﹔有时还要对所取方案作灵敏度分析。图 决策步骤关係图
﹕形成决策问题﹐包括提出方案和确定目标及其效果量度。用概率来定量地描述每个方案所產生的各种结局的可能性。决策者对各种结局的价值定量化﹐一般用效用来表示﹐效用可用效用值来定量。效用值是各决策人根据个人的意志和经验及其所处环境条件等因素﹐对各种结局的价值所作的定量估计。有了效用就能给出偏好。综合分析和评价各方面信息﹐以最后决定方案的取捨﹔有时还要对所取方案作灵敏度分析。图 决策步骤关係图 中示出这4个步骤的相互间关係。
中示出这4个步骤的相互间关係。
常用方法 对於不同的情况有不同的决策方法。确定性情况﹕每一个方案引起一个﹑而且只有一个结局。当方案个数较少时可以用穷举法﹐当方案个数较多时可以用一般最优化方法。随机性情况﹕也称风险性情况﹐即由一个方案可能引起几个结局中的一个﹐但各种结局以一定的概率发生。通常在能用某种估算概率的方法时﹐就可使用随机性决策﹐例如决策树的方法。不确定性情况﹕一个方案可能引起几个结局中的某一个结局﹐但各种结局的发生概率未知。这时可使用不确定型决策﹐例如拉普拉斯準则﹑乐观準则﹑悲观準则﹑遗憾準则等来取捨方案。多目标情况﹕由一个方案同时引起多个结局﹐它们分别属於不同属性或所追求的不同目标。这时一般採用多目标决策方法。例如化多为少的方法﹑分层序列法﹑直接找所有非劣解的方法等。多人决策情况﹕在同一个方案内有多个决策者﹐他们的利益不同﹐对方案结局的评价也不同。这时採用对策论﹑衝突分析﹑群决策等方法。除上述各种方法外﹐还有对结局评价等有模糊性时採用的模糊决策方法和决策分析阶段序贯进行时所採用的序贯决策方法等。