1) graphical solution of inequality
不等式图解
2) settle the inequality
解不等式
4) decoupling inequalities
解耦不等式
1.
sequences, similar with reference [3] proving a decoupling inequalities.
证明了关于独立同分布随机变量序列的加权 U-统计量的一个重对数律 ,类似于文献 [3]证明了一个加权 U-统计量的解耦不等式 。
6) Inequalities Solution
不等式组求解
1.
A Buffer Overflow Detection Based on Inequalities Solution;
一种基于不等式组求解的缓冲区溢出检测
补充资料：不等式
| 不等式 inequality 用不等号将两个解析式连结起来所成的式子。例如x2＋y2≥2xy，sinx≤1，ex＞0 ，2x＜3等 。根据解析式的分类也可对不等式分类，不等号两边的解析式都是代数式的不等式，称为代数不等式；只要有一边是超越式，就称为超越不等式。例如 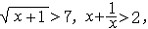 是代数不等式，lg(1＋x)＞x是超越不等式。通常不等式中的数是实数，字母也代表实数，不等式的一般形式为F(x，y，……，z)≤G(x，y，……，z )（其中不等号也可以为＜，≥，＞ 中某一个），两边的解析式的公共定义域称为不等式的定义域，不等式既可以表达一个命题，也可以表示一个问题。例如，平均值不等式定理“x1，x2，……，xn取任意正数时，不等关系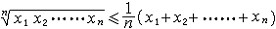 
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |