1) minimum of a quadratic form


二次型的极小值
2) limit of quadratic form


二次型极值
3) qudratic optimization


二次型极值问题
4) double extreme


二次极值
1.
Double limit laws for distributions of double extremes;


二次极值的分布之重极限律
2.
Y~((l))(m, n; k) is called the l-th double extremes of the k-th maxima.


记Y(l)(m,n;k)为{Xm,n;m,n≥1}的第k个上极值之第l个二次极值。
5) quadratic minimization problem


二次型极小化问题
1.
We prove convergence of iterative algorithm with errors to the quadratic minimization problem,which improves the recent results of convergence of iterative algorithm in new condition about quadratic optimization.
证明了二次型极小化问题带误差的迭代算法的有效性,所得结果推广了关于二次型极小化问题迭代的收敛性。
2.
Under new control conditions,we prove convergence of the quadratic minimization problem,which improves the recent results by Xu about quadratic optimization.
在新的控制条件下,证明了二次型极小化问题的迭代算法的有效性,所得结果改进了徐洪坤关于二次型优化的最新结果。
6) Extreme Value of Quadratics of N Variables


n元二次式的极值
补充资料:二次型
| 二次型 quadratic form 线性代数的主要内容之一。起源于解析几何中二次曲线、二次曲面标准方程的研究。设aij取自数域F且aij=a ji(i,j=1,2,…,n),则F上x1,…,xn的二次齐式f(x1,…,xn)= 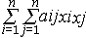 ,称为F上n元二次型,简记为 f,它有矩阵表示f(x1…xn)=(x1…xn)A(x1…xn )′。A=(aij)n=A′由f唯一确定,称为f的矩阵;A的秩称为f的秩。一个只含平方项的二次型称为标准二次型。设P是F上的可逆矩阵,f经变量的可逆代换(x1…xn)=(y1…yn)P′得到的二次型是g(y1…yn),则称g与f等价。每个二次型等价于一个标准二次型。秩为r的复二次型等价于 ,称为F上n元二次型,简记为 f,它有矩阵表示f(x1…xn)=(x1…xn)A(x1…xn )′。A=(aij)n=A′由f唯一确定,称为f的矩阵;A的秩称为f的秩。一个只含平方项的二次型称为标准二次型。设P是F上的可逆矩阵,f经变量的可逆代换(x1…xn)=(y1…yn)P′得到的二次型是g(y1…yn),则称g与f等价。每个二次型等价于一个标准二次型。秩为r的复二次型等价于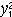 +…+ +…+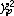 ,从而互不等价的n元复二次型共有n+1类。每个秩r的实二次型有唯一的标准形 ,从而互不等价的n元复二次型共有n+1类。每个秩r的实二次型有唯一的标准形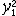 +…+ +…+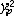 -…- -…- ,从而互不等价的n元实二次型共有(n+1)(n+2)类。与y1+…+yn等价的实二次型称为正定二次型,十分有用。二次型理论在几何、物理等学科有广泛应用。通过坐标的正交变换所得标准形称为主轴形式,它是解析几何问题的自然推广。 ,从而互不等价的n元实二次型共有(n+1)(n+2)类。与y1+…+yn等价的实二次型称为正定二次型,十分有用。二次型理论在几何、物理等学科有广泛应用。通过坐标的正交变换所得标准形称为主轴形式,它是解析几何问题的自然推广。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条