1) base displacement addressing system


基数位移定址系统
2) base displacement address


基数位移定址
3) base displacement addressing


基础位移定址
4) addressing system


定址系统
5) mobile positioning system


移动定位系统
1.
In this paper, we introduce the realization of mobile positioning system, illustrate the working scheme of gpsOne and the scheme of gpsOne on the side of the mobile phone, and actualize the application of “Friends positioning” on the base of gpsOne technology.
介绍了移动定位系统的实现方式,重点阐述了基于gpsOne平台的解决方案和工作方式,以及用于手机的gpsOne方案。
6) Displacement Calculating System


位移标定系统
补充资料:基数
| 基数 cardinal number 集合论中刻画任意集合所含元素数量多少的一个概念。又称势。两个能够建立元素间一一对应的集合称为互相对等集合。例如3个人的集合和3匹马的集合可以建立一 一对应,是两个对等的集合。根据对等这种关系对集合进行分类,凡是互相对等的集合就划入同一类。这样,每一个集合都被划入了某一类 。任意一个集合A所属的类就称为集合A的基数,记作 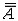 (或|A|,或cardA)。这样,当A 与B同属一个类时,A与B 就有相同的基数,即 (或|A|,或cardA)。这样,当A 与B同属一个类时,A与B 就有相同的基数,即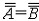 。而当 A与B不同属一个类时,它们的基数也不同。即 。而当 A与B不同属一个类时,它们的基数也不同。即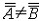 。 如果把单元素集的基数记作1,两个元素的集合的基数记作2,等等,则任一个有限集的基数就与通常意义下的自然数一致 。空集 。 如果把单元素集的基数记作1,两个元素的集合的基数记作2,等等,则任一个有限集的基数就与通常意义下的自然数一致 。空集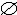 的基数也记作σ 。于是有限集的基数也就是传统概念下的“个数”。但是,对于无穷集,传统概念没有个数,而按基数概念,无穷集也有基数,例如,任一可数集与自然数集N有相同的基数 的基数也记作σ 。于是有限集的基数也就是传统概念下的“个数”。但是,对于无穷集,传统概念没有个数,而按基数概念,无穷集也有基数,例如,任一可数集与自然数集N有相同的基数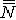 ,即所有可数集是等基数集。不但如此,还可以证明实数集R与可数集的基数不同,即 ,即所有可数集是等基数集。不但如此,还可以证明实数集R与可数集的基数不同,即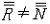 。所以集合的基数是个数概念的推广。基数可以比较大小。假设A,B的基数分别是a,β,即 。所以集合的基数是个数概念的推广。基数可以比较大小。假设A,B的基数分别是a,β,即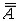 =a, =a,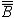 =β,如果A与B的某个子集对等,就称 A 的基数不大于B的基数,记作a≤β,或β≥a。如果 a≤ β,但a≠β( 即A与B不对等 ),就称A的基数小于B的基数,记作a<β,或β>a。基数可以进行运算 。设 =β,如果A与B的某个子集对等,就称 A 的基数不大于B的基数,记作a≤β,或β≥a。如果 a≤ β,但a≠β( 即A与B不对等 ),就称A的基数小于B的基数,记作a<β,或β>a。基数可以进行运算 。设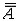 =a , =a ,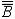 =β,且 A∩B= =β,且 A∩B=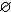 ,则规定 ,则规定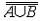 为a 与β之和记作 为a 与β之和记作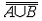 =a +β。设 =a +β。设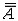 =a, =a,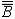 =β,A×B为 A与B的积集,规定 =β,A×B为 A与B的积集,规定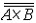 为 a 与β的积,记作 为 a 与β的积,记作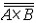 =a·β。 =a·β。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条