1) irregular syllogism
不规则三段论法
2) rule of syllogism
三段论法规则
3) rule of hypothetical syllogism
假言三段论规则
4) rule of extended syllogism
扩充三段论规则
5) rule of syllogism
三段论的规则
6) method of irregular triangulate for earthcalculation(MITEC)
不规则三角形法
补充资料：三段论
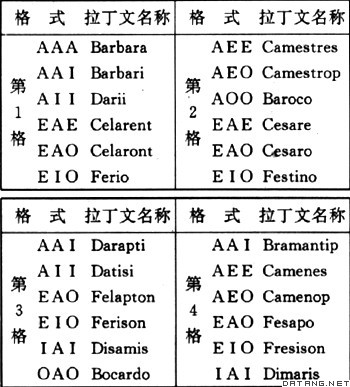
| 三段论 syllogism 传统逻辑中的一类主要推理。又称直言三段论。亚里士多德首先提出了关于三段论的系统理论。 三段论是这样一类推理：它由三个直言命题组成，其中两个是前提，一个是结论；并由三个不同的词项作这些命题的主谓项，而每个词项在两个命题中各出现一次。习惯上以S代表结论的主项(小项)，P代表结论的谓项(大项)，M代表在两前提中出现的词项（中项）；包含小项的前提叫小前提，包含大项的前提叫大前提。 一个三段论是有效的当且仅当符合以下5条规则：①M至少周延一次。②S、P在结论中周延仅当它在前提中周延。③两前提并非都是否定的。④如有一否定的前提则结论也是否定的。⑤如结论是否定的则有一前提也是否定的。除⑤外，这些规则并不都彼此独立。 根据S、M、P在前提中作主谓项的不同情况， 三段论分为以下4个格：  组成三段论的三个直言命题可以有各种形式，由此形成三段论的式，如AAA。其中有的式在任何格里都无效，如EEE；有的式只在某些格里有效。三段论有以下24个有效的形式：
欧洲中世纪逻辑学家为了帮助人们记忆有效的三段论形式及其化归方法，用拉丁文编写了一些口诀，并在大部分单词中嵌入了代表有效式的字母，这些单词就是各有效三段论形式的名称。如Barbara中就嵌入了AAA。这里所列的名称，采自较为常见的一首口诀。 三段论的各种形式中，只有第1格三段论能得到结论SAP，在日常思维中第1格更为自然而习见；第2格只能得到否定的结论，它常用于区别事物；第3格只能得到特称的结论，常用于证明具有某种属性的事物存在。 亚里士多德已充分讨论过三段论的化归问题，建立了人类历史上最早的公理系统之一。他所开创的传统逻辑利用对当关系、换质和换位、归谬法等，把其他格的三段论化归为第1格，并用Barbara证明第1格的其他各式，从而把24个有效的三段论形式组成一个公理系统。 亚里士多德的三段论不考虑指称空类的词项，认为从全称命题可以推出特称命题。现代逻辑为了克服这一不足，把有效的三段论形式加以推广，使得组成三段论的命题可以包含指称空类的词项，由此确认了由9个两全称前提得出特称结论的三段论都是无效的。它进而指出，要从这种前提得到特称结论，就必须增加说明某些类不空的前提。现代逻辑认为三段论有效的充分必要条件应该是：①M恰好周延一次。②S、P各自在结论和前提中的周延情况相同。③前提中和结论中的否定命题数目相同。从现代逻辑的角度看，三段论只是一元谓词逻辑中的一小部分。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条