1) asymptote of a hyperbola


双曲线的渐近线
2) asymptote of curve


曲线的渐近线
3) asymptotic curve


渐近曲线
1.
This paper discussed some other characteristics of asymptotic curve through careful analysis, such as the characteristics of asymptotic curve on the surface of translation, the parallel surface and other surface and draw a conclusion that normal line surface of the asympt.
三维欧氏空间中的渐近曲线是局部微分几何中的一种重要的曲线 ,它有许多重要的性质和应用 ,这些在一般的教科书上都有介绍。
2.
In Minkowski space R~(3,1) by employing the method of moving frames to describe construcions and to make local calculations,the equations about asymptotic direction and asymptotic curve of spacelike surface are obtained,and some corresponding results obtained before are extended and improved.
考虑Minkowski空间R3,1中类空曲面的渐近方向与渐近曲线,采用活动标架的方法进行局部计算和整体结构的刻画,得到了渐近方向与渐近曲线的一般方程,推广并改进了已有的结果,并通过具体例子加以阐述。
3.
In this paper,we discuss parallel surfaces of a surface and obtain the sufficient and necessary condition for geodesic (asymptotic curve) of the surface whose corresponding curve is geodesic(asymptotic one) of the parallel surface.
给出平行曲面上对应曲线同时为测地线( 渐近曲线) 的一个充要条件。
5) asymptote
[英]['æsimptəut] [美]['æsɪm,tot]


渐近线,渐近
6) hyperbola approximation


双曲线近似
1.
A hyperbola approximation approach in the percolation model of the liquid glass transition;
液相-玻璃相转变的渗流模拟中的双曲线近似
补充资料:双曲线
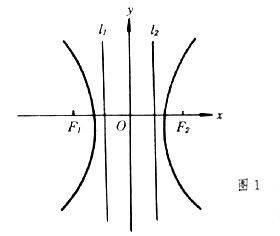
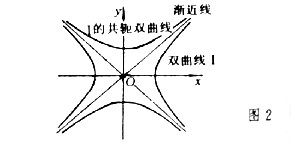
| 双曲线 hyperbola 二次曲线的一种。平面上到两个定点F1、F2的距离之差的绝对值等于一个常数2a的动点的轨迹。定点F1、F2称为双曲线的焦点,两焦点间的距离称为焦距(记为2c)。这个双曲线的标准方程为 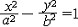 (此处b2=c2-a2)。双曲线有两条互相垂直的对称轴,焦点所在的轴称为实轴,和双曲线不交的轴称为虚轴,分别如图1中的x轴和y轴 。双曲线分为两支,分别位于虚轴的两侧(图1)。标图1准方程中的a,b分别称为双曲线的半实轴长和半虚轴长,a,b相等时,称为等轴双曲线。双曲线有一个对称中心,称为中心,如图1中的坐标原点。双曲线上的动点沿双曲线移向无穷远时,与过中心的两条定直线 (此处b2=c2-a2)。双曲线有两条互相垂直的对称轴,焦点所在的轴称为实轴,和双曲线不交的轴称为虚轴,分别如图1中的x轴和y轴 。双曲线分为两支,分别位于虚轴的两侧(图1)。标图1准方程中的a,b分别称为双曲线的半实轴长和半虚轴长,a,b相等时,称为等轴双曲线。双曲线有一个对称中心,称为中心,如图1中的坐标原点。双曲线上的动点沿双曲线移向无穷远时,与过中心的两条定直线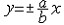 无限接近 ,即距离趋向于零,这两条定直线称为双曲线的渐近线 (图2)。交换双曲线的实轴和虚轴所得的双曲线 无限接近 ,即距离趋向于零,这两条定直线称为双曲线的渐近线 (图2)。交换双曲线的实轴和虚轴所得的双曲线 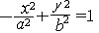 ,称为原来双曲线的共轭双曲线。双曲线和它的共轭双曲线有共同的渐近线(图2)。 双曲线的焦距与实轴长之比 ,称为原来双曲线的共轭双曲线。双曲线和它的共轭双曲线有共同的渐近线(图2)。 双曲线的焦距与实轴长之比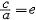 称为双曲线的离心率 。双曲线的离心率大于1,当离心率由小变大时,双曲线开口就由扁狭变得开阔。双曲线也可看成是平面上到定点(焦点)与到定直线(准线)的距离之比(离心率)等于某一大于1的常数的动点的轨迹。双曲线有两条准线(图1),对于焦点F1,相应的准线是l1 ,对于焦点F2,相应的准线是l2 称为双曲线的离心率 。双曲线的离心率大于1,当离心率由小变大时,双曲线开口就由扁狭变得开阔。双曲线也可看成是平面上到定点(焦点)与到定直线(准线)的距离之比(离心率)等于某一大于1的常数的动点的轨迹。双曲线有两条准线(图1),对于焦点F1,相应的准线是l1 ,对于焦点F2,相应的准线是l2
|
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条