1) mechanical testing instrument


力学测试仪器
2) optical testing instrument


光学测试仪器
3) Mechanical measuring instrument


力学测量仪器
4) measurement instrument


测试仪器
1.
The design of remote control keyboard for optoelectronic measurement instruments;


光电测试仪器遥控键盘的设计
2.
Design and realization of P&P technology in intelligent measurement instruments;


即插即用技术在智能测试仪器中的设计与实现
3.
The new development situation of software defined radio(SDR) in measurement instruments is analysed.
分析了目前软件无线电在测量仪器领域发展的新趋势,并以N5530S测量接收机系统为例介绍了软件无线电在测试仪器及系统中的应用原理及方法。
6) testing apparatus


测试仪器
1.
The discussion of the reliability of the GB6566-2001 standard test method and correlation testing apparatus;
关于GB6566-2001标准试验方法及相关测试仪器可靠性的讨论
补充资料:力学
| 力学 mechanics 研究物质机械运动规律的科学。自然界物质有多种层次,从宇观的宇宙体系,宏观的天体和常规物体,细观的颗粒、纤维、晶体,到微观的分子、原子、基本粒子。通常理解的力学以研究天然的或人工的宏观对象为主。但由于学科的互相渗透,有时也涉及宇观或细观甚至微观各层次中的对象以及有关的规律。机械运动亦即力学运动是物质在时间、空间中的位置变化,包括移动、转动、流动、变形、振动、波动、扩散等,而平衡或静止,则是其中的一种特殊情况。机械运动是物质运动的最基本的形式。物质运动的其他形式还有热运动、电磁运动、原子及其内部的运动和化学运动等。机械运动常与其他运动形式共同存在,只是在研究力学问题时突出地考虑机械运动这种形式罢了;如果其他运动形式对机械运动有较大影响,或者需要考虑它们之间的相互作用,便会在力学同其他学科之间形成交叉学科或边缘学科。力是物质间的一种相互作用,机械运动状态的变化是由这种相互作用引起的。静止和运动状态不变,都意味着各作用力在某种意义上的平衡。力学,可以说是力和(机械)运动的科学。 力学在汉语中的意思是力的科学。汉语“力”字最初表示的是手臂使劲,后来虽又含有他义,但都同机械或运动没有直接联系。“力学”一词译自英语mechanics(源于希腊语 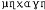 ——机械)。mechanics在19世纪50年代作为研究力的作用的学科名词传入中国时,译作重学,后来改译作力学。 ——机械)。mechanics在19世纪50年代作为研究力的作用的学科名词传入中国时,译作重学,后来改译作力学。发展简史 力学知识最早起源于对自然现象的观察和在生产劳动中的经验。人们在建筑、灌溉等劳动中使用杠杆、斜面、汲水器具,逐渐积累起对平衡物体受力情况的认识。古希腊的阿基米德对杠杆平衡、物体重心位置、物体在水中受到的浮力等作了系统研究,确定它们的基本规律,初步奠定了静力学即平衡理论的基础。古代人还从对日、月运行的观察和弓箭、车轮等的使用中了解一些简单的运动规律,如匀速的移动和转动。但是对力和运动之间的关系,只是在欧洲文艺复兴时期以后才逐渐有了正确的认识。伽利略在实验研究和理论分析的基础上,最早阐明自由落体运动的规律,提出加速度的概念。I.牛顿继承和发展前人的研究成果(特别是J.开普勒的行星运动三定律),提出物体运动三定律。伽利略、牛顿奠定了动力学的基础。牛顿运动定律的建立标志着力学开始成为一门科学。此后力学的进展在于它所考虑的对象由单个的自由质点转向受约束的质点和受约束的质点系;这方面的标志是J.le R.达朗贝尔提出的达朗贝尔原理和J.-L.拉格朗日建立的分析力学。L.欧拉又进一步把牛顿运动定律推广用于刚体和理想流体的运动方程。欧拉建立理想流体的力学方程可看作是连续介质力学的肇端。在此以前,有关固体的弹性、流体的粘性、气体的可压缩性等的物质属性方程已经陆续建立。运动定律和物性定律这两者的结合,促使弹性固体力学基本理论和粘性流体力学基本理论孪生于世,在这方面作出贡献的是C.-L.-M.-H.纳维、A.-L.柯西、S.-D.泊松、G.G.斯托克斯等人。弹性力学和流体力学基本方程的建立,使得力学逐渐脱离物理学而成为独立学科。另一方面,从拉格朗日分析力学基础上发展起来的哈密顿体系,继续在物理学中起作用。从牛顿到哈密顿的理论体系组成物理学中的经典力学或牛顿力学。在弹性和流体基本方程建立后,所给出的方程一时难于求解,工程技术中许多应用力学问题还须依靠经验或半经验的方法解决。这使得19世纪后半叶在材料力学、结构力学同弹性力学之间,水力学和水动力学之间一直存在着风格上的显著差别。到20世纪初,在流体力学和固体力学中,实际应用同数学理论的上述两个方面开始结合,此后力学便蓬勃发展起来,创立了许多新的理论,同时也解决了工程技术中大量的关键性问题,如航空工程中的声障问题和航天工程中的热障问题。这种理论和实际密切结合的力学的先导者是L.普朗特和T.von卡门。他们在力学研究工作中善于从复杂的现象中洞察事物本质,又能寻找合适的解决问题的数学途径,逐渐形成一套特有的方法。从20世纪60年代起,电子计算机应用日广,力学无论在应用上或理论上都有了新的进展。力学继承它过去同航空和航天工程技术结合的传统,在同其他各种工程技术以及同自然科学的其他学科的结合中,开拓自己新的应用领域。70年代以来混沌理论方面的进展,说明确定性动力学系统中广泛存在长期不可预测性,使人们对于以牛顿运动定律为基础的经典力学有了新的认识。 力学在中国的发展经历了一个特殊的过程。与古希腊几乎同时,中国古代对平衡和简单的运动形式就已具备相当水平的力学知识,所不同的是未建立起像阿基米德那样的理论系统。在文艺复兴前的约1000年时间内,整个欧洲的科学技术进展缓慢,而中国科学技术的综合性成果卓著,其中有些在当时世界居于领先地位。这些成果反映出丰富的力学知识,但终未形成系统的力学理论。明末清初,中国科学技术已显著落后于欧洲。经过曲折的过程,到19世纪中叶,牛顿力学才由欧洲传入中国。以后,中国力学的发展便随同世界潮流前进。 学科性质 力学原是物理学的一个分支。物理科学的建立则是从力学开始的。在物理科学中,人们曾用纯粹力学理论解释机械运动以外的各种形式的运动,如热、电磁、光、分子和原子内的运动等。当物理学摆脱了这种机械(力学)的自然观而获得健康发展时,力学则在工程技术的推动下按自身逻辑进一步演化,逐渐从物理学中独立出来。20世纪初,相对论指出牛顿力学不适用于速度接近光速或者宇宙尺度内的物体运动;20年代,量子论指出牛顿力学不适用于微观世界。这反映人们对力学认识的深化,即认识到物质在不同层次上的机械运动规律是不同的。通常理解的力学只以研究宏观的机械运动为主,因而有许多带“力学”名称的学科如热力学、统计力学、相对论力学、电动力学、量子力学等在习惯上被认为是物理学的分支,而不属于力学的范围。但由于历史上的原因,力学和物理学仍有着特殊的亲缘关系,特别是在以上各力学分支和牛顿力学之间,许多概念、方法、理论都有不少相似之处。 力学与数学在发展中始终相互推动,相互促进。一种力学理论往往和相应的一个数学分支相伴产生,如运动基本定律和微积分,运动方程的求解和常微分方程,弹性力学及流体力学的基本方程和数学分析理论,天体力学中运动稳定性和微分方程定性理论等。有人甚至认为力学是一门应用数学。但是力学和物理学一样,还有需要实验基础的一面,而数学寻求的是比力学更带普遍性的数学关系,两者有各自的研究对象。 力学同物理学、数学等学科一样,是一门基础科学,它所阐明的规律带有普遍的性质。 力学又是一门技术科学,它是许多工程技术的理论基础,又在广泛的应用过程中不断得到发展。当工程学还只分民用工程学(即土木工程学)和军事工程学两大分支时,力学在这两个分支中已起着举足轻重的作用。工程学越分越细,各个分支中许多关键性的进展都有赖于力学中有关运动规律、强度、刚度等问题的解决。力学和工程学的结合促使工程力学各个分支的形成和发展。无论是历史较久的土木工程、建筑工程、水利工程、机械工程、船舶工程等,还是后起的航空工程、航天工程、核技术工程、生物医学工程等,都或多或少有工程力学的活动场地。力学作为一门技术科学,并不能代替工程学,只指出工程技术中解决力学问题的途径,而工程学则从更综合的角度考虑具体任务的完成。同样地,工程力学也不能代替力学,因为力学还有探索自然界一般规律的任务。
力学既是基础科学又是技术科学这种二重性,有时难免会引起侧重基础研究一面和侧重应用研究一面的力学家之间的不同看法。这种二重性使力学家为沟通人类认识自然和改造自然两个方面作出了贡献。 研究方法 力学研究方法遵循认识论的基本法则:实践—现—理论—实践。力学作为基础科学和作为技术科学从不同侧面反映这个法则。力学家们根据对自然现象的观察,特别是定量观测的结果,根据生产过程中积累的经验和数据,或者根据为特定目的而设计的科学实验的结果,提炼出量与量之间的定性的或数量的关系。为了使这种关系反映事物的本质,力学家要善于抓住起主要作用的因素,摒弃或暂时摒弃一些次要因素。力学中把这种过程称为建立模型。质点、质点系、刚体、弹性固体、粘性流体、连续介质等是各种不同的模型。在模型的基础上可以运用已知的力学的或物理学的规律(必要时作一些假设)以及合适的数学工具进行理论上的演绎工作,导出新的结论。在理论演绎中,为了使理论具有更高的概括性和更广泛的适用性,往往采用一些无量纲参数如雷诺数、马赫数、泊松比等。这些参数既反映物理本质,又是单纯的数字,不受尺寸、单位制、工程性质、实验装置类型的牵制。依据第一个实践环节所得理论结论建立的模型是否合理,有待于新的观测、工程实践或者科学实验等第二个实践环节加以验证。采用上述无量纲参数以及通过有关的量纲分析使得这种验证能在更广泛的范围内进行。对一个单独的力学课题或研究任务来说,这种实践和理论环节不一定能分得很清,也可能和其他课题或任务的某个环节相互交叉,相互影响。课题或任务中每一项具体工作又可能只涉及一个环节或者一个环节的一部分。因此,从局部看来,力学研究工作方式是多样的:有些只是纯数学的推理,甚至着眼于理论体系在逻辑上的完善化;有些着重数值方法和近似计算;有些着重实验技术;有些着重在天文观测和考察自然现象中积累数据;而更大量的则是着重在运用现有力学知识来解决工程技术中或探索自然界奥秘中提出的具体问题。每一项工程又都需要具备自身有关的知识和其他学科的配合。数学推理需要各种现代数学知识,包括一些抽象数学分支的知识。数值方法和近似计算要了解计算技术、计算数学。现代的力学实验设备,诸如大型的风洞、水洞,它们的建立和使用本身就是一个综合性的科学技术项目,需要多工种、多学科的协作。应用研究更需要对应用对象的工艺过程、材料性质、技术关键等有清楚的了解。在力学研究中既有细致的、独立的分工,又有综合的、全面的协作。从力学研究和对力学规律认识的整体来说,实践是检验理论正确与否的唯一标准。以上各种工作都是力学研究不可缺少的部分。
分支学科 力学的各分支学科是由于研究方法以及研究对象的不同而形成的,它可粗分为静力学、运动学和动力学三部分,也可区分为固体力学、流体力学和一般力学三个分支。它又可按研究时所采用的主要手段分为理论分析、实验研究和数值计算3个方面。力学与工程技术和其他自然科学方面的结合形成工程力学或应用力学各分支以及多种交叉学科,诸如土力学、工业空气动力学、生物力学、地质力学等。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条

