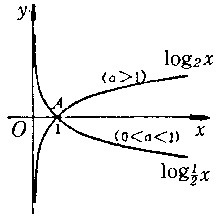1) function analog computer


函数模拟计算机
2) functional analog computer


函数式模拟计算机
3) computer simulation


计算机数值模拟
1.
The second part, Introducting attract grid into evacuation cellular automaton model, through simulating occupant evacuation process in corridor of building, computer simulation results show that each room is the obvious difference in the evacuation of pedestrians,it is the width of each room that the process of entire evacuation is less affected, and each room location of the evacua
第二部分,引入格点吸引度的概念建立了人员疏散元胞自动机模型,对建筑物走廊内的人员疏散过程进行了模拟研究,计算机数值模拟结果表明,此模型能很好地再现行人在走廊的疏散全过程,各房间内的行人疏散时间有明显的差异,房间出口宽度对整个疏散的影响较小,而房间出口位置对疏散的影响较大,房间出口越靠近走廊出口方向越能缩短疏散时间。
2.
Ordinary high-rise residential kitchen computer simulation in Central Exhaust System


论文在理论分析的基础上,运用计算机数值模拟的方法,选取典型的30层高层住宅厨房集中排烟道模型模拟分析排烟道排风质量,分析排风量不足、不平衡的原因,并针对解决的思路及方法进行探讨。
4) computer numerical simulation


计算机数值模拟
1.
Based on production practice and computer numerical simulation, the merits and demerits of each program are summarized.
对比分析了石油装备钻机、修井机提升系统上使用的关键部件钩体的几种铸造工艺方案,经过生产实践和借助先进计算机数值模拟软件,总结出了每种铸造工艺方案的优势和劣势。
2.
For an example of craft design about stamping forming of the gate of a certain railway freight car, formulize the craft calculation of fluctuate formation on a weathering steel plate of moderate thickness, and the method and course of simulating analysis about forming process using computer numerical simulation technology.
以某型铁路货车车门冲压成形工艺设计为例,阐述了耐候钢中厚板起伏成形的工艺计算以及利用计算机数值模拟技术进行成形过程的仿真分析的方法及过程。
3.
In this paper,an integrated method combined with thermodynamic simulation,microcosmic simulation and computer numerical simulation is put forward to study the mechanism and rules of metal hot forming.
针对以往对金属热成形过程和组织性能控制的研究存在许多困难和不足,提出了用热力学模拟、微观模拟和计算机数值模拟综合集成的方法研究金属材料热成形的机制与规律,为工艺过程和产品质量的科学控制以及新技术的开发提供依据。
6) analog-digitalcomputer


模(拟)—数(字)计算机
补充资料:函数
| 函数 functions 数学中的一种对应关系,是从某集合A到实数集B的对应。简单地说,甲随着乙变,甲就是乙的函数。精确地说,设X是一个不空集合,Y是某个实数集合,f是个规则,若对X中的每个x,按规则f,有Y中的一个y与之对应,就称f是X上的一个函数,记作y=f(x),称X为函数f(x)的定义域,Y为其值域,x叫做自变量,y为因变量。 例1:y=sinx X=[0,2π],Y=[-1,1],它给出了一个函数关系。当然,把Y改为Y1=(a,b),a<b为任意实数,仍然是一个函数关系。 例2:某商场一年12个月毛线的零售量(单位:百千克)变化,见表1。
例3:某河道的一个断面图如图1所示。
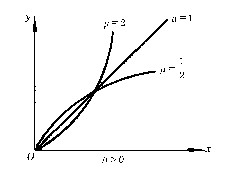
其深度y与一岸边点O到测量点的距离x之间的对应关系呈曲线,这代表一个函数,定义域为[0,b]。以上3例展示了函数的三种表示法:公式法,表格法和图像法。 复合函数 有3个变量,y是u的函数,y=ψ(u),u是x的函数,u=f(x),往往能形成链:y通过中间变量u构成了x的函数: x→u→y,这要看定义域:设ψ的定义域为U。f的值域为U,当U*ÍU时,称f与ψ构成一个复合函数,例如y=lgsinx,x∈(0,π)。此时sinx>0,lgsinx有意义。但如若规定x∈(-π,0),此时sinx<0,lgsinx无意义,就成不了复合函数。 反函数 就关系而言,一般是双向的,函数也如此,设y=f(x)为已知的函数,若对每个y∈Y,有唯一的x∈X,使f(x)=y,这是一个由y找x的过程,即x成了y的函数,记为x=f -1(y)。称f -1为f的反函数。习惯上用x表示自变量,故这个函数仍记为y=f -1(x),例如y=sinx与y=arcsinx互为反函数。在同一坐标系中,y=f(x)与y=f -1(x)的图形关于直线y=x对称。 隐函数 若能由函数方程F(x,y)=0确定y为x的函数y=f(x),即F(x,f(x))≡0,就称y是x的隐函数。 多元函数 设点(x1,x2,…,xn)∈GÍRn,UÍR1,若对每一点(x1,x2,…,xn)∈G,由某规则f有唯一的u∈U与之对应:f:G→U,u=f(x1,x2,…,xn),则称f为一个n元函数,G为定义域,U为值域。 基本初等函数及其图像 幂函数、指数函数、对数函数、三角函数、反三角函数称为基本初等函数。 ①幂函数:y=xμ(μ≠0,μ为任意实数)定义域:μ为正整数时为(-∞,+∞),μ为负整数时是(-∞,0)∪(0,+∞);μ= 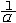 (α为整数),当α是奇数时为(-∞,+∞),当α是偶数时为(0,+∞);μ=p/q,p,q互素,作为 (α为整数),当α是奇数时为(-∞,+∞),当α是偶数时为(0,+∞);μ=p/q,p,q互素,作为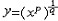 的复合函数进行讨论。略图如图2、图3。 的复合函数进行讨论。略图如图2、图3。
②指数函数:y=ax(a>0,a≠1),定义成为(-∞,+∞),值域为(0,+∞),a>0时是严格单调增加的函数(即当x2>x1时, 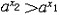 ),0<a<1时是严格单减函数。对任何a,图像均过点(0,1),注意y=ax和y=( ),0<a<1时是严格单减函数。对任何a,图像均过点(0,1),注意y=ax和y=(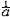 )x的图形关于y轴对称。如图4。 )x的图形关于y轴对称。如图4。
③对数函数:y=logax(a>0),称a为底,定义域为(0,+∞),值域为(-∞,+∞)。a>1时是严格单调增加的,0<a<1时是严格单减的。不论a为何值,对数函数的图形均过点(1,0),对数函数与指数函数互为反函数。如图5。
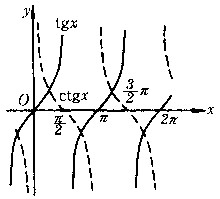
④三角函数:见表2。
正弦函数、余弦函数如图6,图7所示。
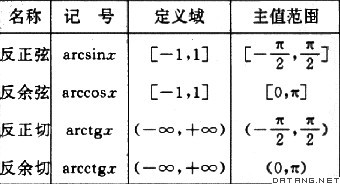
⑤反三角函数:见表3。双曲正、余弦如图8。
⑥双曲函数:双曲正弦 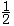 (ex-e-x),双曲余弦(ex+e-x),双曲正切(ex-e-x)/(ex+e-x),双曲余切(ex+e-x)/(ex-e-x)。 (ex-e-x),双曲余弦(ex+e-x),双曲正切(ex-e-x)/(ex+e-x),双曲余切(ex+e-x)/(ex-e-x)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条