1) complex calculus


复变微积分学
2) calculus
[英]['kælkjələs] [美]['kælkjələs]


微积分学
1.
The Teaching of Calculus and the Improving of the Studying Spirit of Students;


《微积分学》教学与调动学生学习积极性
2.
Appling Calculus to Solve Maximum and minimum of the Polybasic Funtion;


微积分学在多元函数最值问题中的应用
3.
With the help of the examples accumulates in the teaching process,this paper reveals all the uses of calculus in solving some primary problems.
以教学过程中积累的多个例子作简单的讨论,展示了微积分学在解决初等问题中的各类应用。
3) new calculus


新微积分学
5) variational-integral perturbation method


变分-积分微扰法
1.
The improved variational-perturbation method based on integral equation(variational-integral perturbation method) is applied to solve the quartic anharmonic oscillator in the ground state.
利用基于积分方程的改进的变分微扰方法(变分-积分微扰法)求解四次方非谐振子基态。
2.
We employ the improved variational-perturbation method based on integral equation (variational-integral perturbation method) to solve the heavy quarkonium in the 2S state.
利用基于积分方程的改进的变分微扰方法(变分-积分微扰法)求解重夸克偶素激发态。
6) calculus
[英]['kælkjələs] [美]['kælkjələs]


微积分,算法,微积分学
补充资料:微积分学
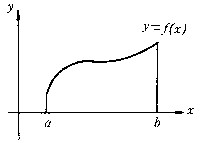
| 微积分学 differential and integral calculus 数学中的基础分支。内容主要包括函数、极限、微分学、积分学及其应用。函数是微积分研究的基本对象,极限是微积分的基本概念,微分和积分是特定过程特定形式的极限。17世纪后半叶,英国数学家I.牛顿和德国数学家G.W.莱布尼兹,总结和发展了几百年间前人的工作,建立了微积分,但他们的出发点是直观的无穷小量,因此尚缺乏严密的理论基础。19世纪A.-L.柯西和K.魏尔斯特拉斯把微积分建立在极限理论的基础上;加之19世纪后半叶实数理论的建立,又使极限理论有了严格的理论基础,从而使微积分的基础和思想方法日臻完善。 极限的思想方法可追溯到古代,3世纪,中国数学家刘徽创立的割圆术用圆内接正九十六边形的面积近似代替圆面积,求出圆周率π的近似值3.141024,并指出:“割之弥细,所失弥少 ,割之又割,以至不可割,则与圆合体而无所失矣”。刘徽对面积的深刻认识和他的割圆术方法,正是极限思想的具体体现 。数列极限是函数极限的基础, 一个数列an如果当n无限增大时,an与某一实数无限接近,就称之为收敛数列,a为数列的极限,记作 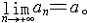 例如,数列 例如,数列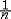 的极限为0。 的极限为0。微分学的基本概念是导数。导数是从速度问题和切线问题抽象出来的数学概念。牛顿从苹果下落时越落越快的现象受到启发,希望用数学工具来刻画这一事实。若用s=s(t)表示物体的运动规律,即物体运动中所走路程s与时间t的关系,那么物体在t=t0时的瞬时速度为v(t0)= 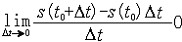 ,并记v(t0)=s′(t0),并称之为路程s关于时间t的导数或变化率 ,也可记v(t0)=( ,并记v(t0)=s′(t0),并称之为路程s关于时间t的导数或变化率 ,也可记v(t0)=(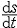 )|t=t0。而物体运动的加速度 a(t)=v′(t)=s″(t)=( )|t=t0。而物体运动的加速度 a(t)=v′(t)=s″(t)=(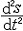 )。导数作为一个数学工具无论在理论上还是实际应用中,都起着基础而重要的作用。例如在求极大、极小值问题中的应用。 )。导数作为一个数学工具无论在理论上还是实际应用中,都起着基础而重要的作用。例如在求极大、极小值问题中的应用。积分学的基本概念是一元函数的不定积分和定积分。主要内容包括积分的性质、计算,以及在理论和实际中的应用。不定积分概念是为解决求导和微分的逆运算而提出来的。如果对每一x∈I ,有f(x)=F′(x),则称F(x)为f(x)的一个原函数,f(x)的全体原函数叫做不定积分,记为 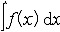 ,因此,如果F(x)是 f(x)的一个原函数,则 ,因此,如果F(x)是 f(x)的一个原函数,则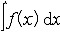 =F(x)+C,其中C为任意常数。定积分概念的产生来源于计算平面上曲边形的面积和物理学中诸如求变力所作的功等物理量的问题。解决这些问题的基本思想是用有限代替无限;基本方法是在对定义域[a,b]进行划分后,构造一个特殊形式的和式,它的极限就是所要求的量。具体地说,设f(x)为定义在[a,b]上的函数,任意分划区间[a,b]:a=x0<x1<…<xn=b,记 =F(x)+C,其中C为任意常数。定积分概念的产生来源于计算平面上曲边形的面积和物理学中诸如求变力所作的功等物理量的问题。解决这些问题的基本思想是用有限代替无限;基本方法是在对定义域[a,b]进行划分后,构造一个特殊形式的和式,它的极限就是所要求的量。具体地说,设f(x)为定义在[a,b]上的函数,任意分划区间[a,b]:a=x0<x1<…<xn=b,记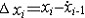 ,||Δ||= ,||Δ||=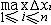 ,任取 xi ∈Δxi,如果有一实数I,有下式成立 : ,任取 xi ∈Δxi,如果有一实数I,有下式成立 :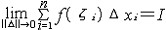 ,则称I为f(x)在[a,b]上的定积分,记为I= ,则称I为f(x)在[a,b]上的定积分,记为I=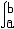 f(x)dx。当f(x)≥0时,定积分的几何意义是表示由x=a,x=b,y=0和y=f(x)所围曲边形的面积。定积分除了可求平面图形的面积外,在物理方面的应用主要有解微分方程的初值问题和“微元求和”。 f(x)dx。当f(x)≥0时,定积分的几何意义是表示由x=a,x=b,y=0和y=f(x)所围曲边形的面积。定积分除了可求平面图形的面积外,在物理方面的应用主要有解微分方程的初值问题和“微元求和”。
联系微分学和积分学的基本公式是:若f(x)在[a,b]上连续,F(x)是f(x)的原函数,则 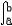 f(x)dx=F(b)-F(a)。通常称之为牛顿-莱布尼兹公式。因此,计算定积分实际上就是求原函数,也即求不定积分。但即使f(x)为初等函数,计算不定积分的问题也不能完全得到解决,所以要考虑定积分的近似计算,常用的方法有梯形法和抛物线法。 f(x)dx=F(b)-F(a)。通常称之为牛顿-莱布尼兹公式。因此,计算定积分实际上就是求原函数,也即求不定积分。但即使f(x)为初等函数,计算不定积分的问题也不能完全得到解决,所以要考虑定积分的近似计算,常用的方法有梯形法和抛物线法。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条