1) coupling mechanis
耦合器;联接机构
2) catenation
[英][,kæti'neiʃən] [美][,kætə'neʃən]
耦合联接联接器
3) coupler
[英]['kʌplə] [美]['kʌplɚ]
联接器;耦合器
5) catheter
[英]['kæθɪtə(r)] [美]['kæθətɚ]
耦合，联接
6) mechanical coupling
机械耦合，机械联接
补充资料：耦合
jj ouhe
耦合
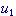coupling
由给定电子组态确定多个价电子原子的能量状态的一种近似方法。它适用于原子中各价电子间的静电斥力势能之和远小于各价电子的自旋轨道磁相互作用能之和的情况,单个电子的轨道角动量[pli]
将和其自旋角动量[psi]
耦合成该电子的总角动量[pji]
,[580-20]
,
是第
个价电子的总角动量量子数，
=
/2
,是普朗克常数。
以两个非等效电子为例,设电子组态为(
),、和 、分别为两电子的主量子数和轨道量子数,电子的自旋量子数都为1/2,即
==1/2,[kg2]
按原子的矢量模型，电子轨道角动量 [pli]与自旋角动量 [psi]耦合，[580-21]
[580-02]
[580-22]
[580-100]
[580-03]
。原子 耦合的多重谱项则由各种可能的()确定,不同谱项间能量差别相对来说比较大,而两电子间静电作用使[580-101]
与[580-1]
耦合成原子的总角动量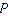
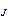，P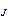＝[580-101]＋[580-1],
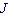为原子总角动量量子数,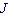＝+,+-1,…，|-|，[kg2]由于这种静电作用远小于电子的轨道与自旋相互作用，因此同一多重谱项中由于电子间静电作用而引起的不同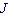值的能态间距是很小的
耦合形成的原子态符号是() 。
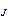对于等效电子（见原子结构），耦合时要考虑泡利不相容原理，所形成的原子态要比非等效电子形成的原子态少。例如两个等效p电子经耦合只能形成[580-04]
、[580-05]
、[580-06]
五种原子态，而两个非等效p电子经耦合将形成[580-07]
、[580-15]
、[580-08]
和[580-09]
等十个原子态。
耦合常适用于确定重元素原子的受激态和轻元素原子的高受激态，有时还适用于确定重元素的基态（例如Pb原子的基态）。
宋增福 曹建庭
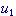耦合 coupling由给定电子组态确定多个价电子原子的能量状态的一种近似方法。它适用于原子中各价电子间的静电斥力势能之和远小于各价电子的自旋轨道磁相互作用能之和的情况,单个电子的轨道角动量[pli]
将和其自旋角动量[psi]耦合成该电子的总角动量[pji],[580-20],是第个价电子的总角动量量子数，=/2,是普朗克常数。以两个非等效电子为例,设电子组态为(
),、和 、分别为两电子的主量子数和轨道量子数,电子的自旋量子数都为1/2,即==1/2,[kg2]按原子的矢量模型，电子轨道角动量 [pli]与自旋角动量 [psi]耦合，[580-21][580-02][580-22][580-100][580-03]。原子 耦合的多重谱项则由各种可能的()确定,不同谱项间能量差别相对来说比较大,而两电子间静电作用使[580-101]与[580-1]耦合成原子的总角动量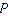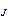，P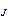＝[580-101]＋[580-1],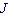为原子总角动量量子数,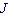＝+,+-1,…，|-|，[kg2]由于这种静电作用远小于电子的轨道与自旋相互作用，因此同一多重谱项中由于电子间静电作用而引起的不同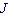值的能态间距是很小的耦合形成的原子态符号是() 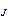。对于等效电子（见原子结构），耦合时要考虑泡利不相容原理，所形成的原子态要比非等效电子形成的原子态少。例如两个等效p电子经
耦合只能形成[580-04]、[580-05]、[580-06]五种原子态，而两个非等效p电子经耦合将形成[580-07]、[580-15]、[580-08]和[580-09]等十个原子态。耦合常适用于确定重元素原子的受激态和轻元素原子的高受激态，有时还适用于确定重元素的基态（例如Pb原子的基态）。宋增福 曹建庭
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条