1) natural-function generator


自然函数产生器
2) natural-function generator


解析函数发生器,自然函数编辑程序
4) Systems Effects of Productive Factors (SEPF)


生产函数国家自然科学基金
5) generator of symmetric function


对称函数产生器
6) special function generator


专用函数产生器
补充资料:解析函数
| 解析函数 analytic function 区域  上处处可微分的复函数。17世纪,L.欧拉和J.leR.达朗贝尔在研究水力学时已发现平面不可压缩流体的无旋场的势函数Φ(x,y)与流函数Ψ(x,y)有连续的偏导数,且满足微分方程组 上处处可微分的复函数。17世纪,L.欧拉和J.leR.达朗贝尔在研究水力学时已发现平面不可压缩流体的无旋场的势函数Φ(x,y)与流函数Ψ(x,y)有连续的偏导数,且满足微分方程组 ,并指出f(z)=Φ(x,y)+iΨ(x,y)是可微函数,这一命题的逆命题也成立。柯西把区域 ,并指出f(z)=Φ(x,y)+iΨ(x,y)是可微函数,这一命题的逆命题也成立。柯西把区域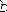 上处处可微的复函数称为单演函数,后人又把它们称为全纯函数、解析函数。B.黎曼从这一定义出发对复函数的微分作了深入的研究,后来,就把上述的偏微分方程组称为柯西-黎曼方程,或柯西-黎曼条件。K. 魏尔斯特拉斯将一个在圆盘上收敛的幂级数的和函数称为解析函数,而区域上的解析函数是指在区域内每一小圆邻域上都能表成幂级数的和的函数。关于解析函数的不同定义在20世纪初被证明是等价的。基于魏尔斯特拉斯的定义,区域上的解析函数可以看作是其内任一小圆邻域上幂级数的解析开拓 ,关于解析开拓的一般定义是,f(z)与g(z)分别是D与D*上的解析函数,若DÉD* ,且在D*上f(z)=g(z)。则称f(z)是g(z)由D*到D的解析开拓 。解析开拓的概念可以推广到这样的情形 :f(z)与g(z)分别是两个圆盘D1与D2上的幂级数,且D1∩D2≠ 上处处可微的复函数称为单演函数,后人又把它们称为全纯函数、解析函数。B.黎曼从这一定义出发对复函数的微分作了深入的研究,后来,就把上述的偏微分方程组称为柯西-黎曼方程,或柯西-黎曼条件。K. 魏尔斯特拉斯将一个在圆盘上收敛的幂级数的和函数称为解析函数,而区域上的解析函数是指在区域内每一小圆邻域上都能表成幂级数的和的函数。关于解析函数的不同定义在20世纪初被证明是等价的。基于魏尔斯特拉斯的定义,区域上的解析函数可以看作是其内任一小圆邻域上幂级数的解析开拓 ,关于解析开拓的一般定义是,f(z)与g(z)分别是D与D*上的解析函数,若DÉD* ,且在D*上f(z)=g(z)。则称f(z)是g(z)由D*到D的解析开拓 。解析开拓的概念可以推广到这样的情形 :f(z)与g(z)分别是两个圆盘D1与D2上的幂级数,且D1∩D2≠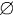 ,在D1∩D2上f(z)=g(z )则也称f与g互为解析开拓,把可以互为解析开拓的( f(z),Δ)的解析圆盘Δ全连起来,作成一个链。它们的并记作Ω,得到了Ω上的一个解析函数,称它为魏尔斯特拉斯的完全解析函数,这里可能出现这样的情形,在连成一个链的圆盘中,有一些圆盘重叠在一起,但在这些重叠圆盘的每一个上的解析函数都是不一样的,它们的每一个都称为完全解析函数的分支。这样的完全解析函数实际是一个多值函数。黎曼提出将多值解析函数中的那些重叠的圆盘看作是不同的“叶”,不使他们在求并的过程中只留下一个代表,于是形成了一种称为黎曼面的几何模型。将多值函数看作是定义于其黎曼曲面上的解析函数,这样多值解析函数变成了单值解析函数。 ,在D1∩D2上f(z)=g(z )则也称f与g互为解析开拓,把可以互为解析开拓的( f(z),Δ)的解析圆盘Δ全连起来,作成一个链。它们的并记作Ω,得到了Ω上的一个解析函数,称它为魏尔斯特拉斯的完全解析函数,这里可能出现这样的情形,在连成一个链的圆盘中,有一些圆盘重叠在一起,但在这些重叠圆盘的每一个上的解析函数都是不一样的,它们的每一个都称为完全解析函数的分支。这样的完全解析函数实际是一个多值函数。黎曼提出将多值解析函数中的那些重叠的圆盘看作是不同的“叶”,不使他们在求并的过程中只留下一个代表,于是形成了一种称为黎曼面的几何模型。将多值函数看作是定义于其黎曼曲面上的解析函数,这样多值解析函数变成了单值解析函数。
多复变量解析函数也有两种定义:①如果一个多复变量函数对其每一个变量都是单变量解析函数,则称其为多复变量解析函数。②若一个多复变函数在每一个“点”(2n维空间中的点)的一个邻域上都可以展成一个多元幂级数,则称其为多复量变解析函数。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
