1) vector
[英]['vektə(r)] [美]['vɛktɚ]


向量,矢量
2) vector
[英]['vektə(r)] [美]['vɛktɚ]


矢量;向量
3) vector
[英]['vektə(r)] [美]['vɛktɚ]


矢量,向量
4) vector quantity


向量;矢量
5) normal vector


法向矢量
1.
The Median Theorem will be applied to determining the normal vector of the point on parabola and then using the technology of tip compensation to measure the parabola accurately.
确定抛物曲线面上所测量点的法向矢量,启动测量针半径补偿作精密测量,使用DEAPPL语言设计程序组,阐述进入CAD/CAM中的数据文件组生成,探讨等距值d对测量精度的影响,在测量机上快速完成二维曲线的测绘和检验,设计的程序组通过标准球实验,测量精度高,除能完成抛物线检验外,还能用于其它精密二维曲线扫描。
2.
In this paper, first introduces about normal vector and then deals with how the stylus regulating automatically its own level on contact complex surface and holds constant level with nominal deflection.
首先介绍了法向矢量在仿形扫描中的作用 ,然后提出了名义偏倾值 DN 的概念 ,及引入名义偏倾值 DN 后在解决扫描中脱模的原理及实现 ,最后介绍了仿形加工及数字化在模具加工中的差异和应注意的问题。
3.
Our method uses object surface normal vectors to obtain vector distances between 3D objects.
本文提出了基于B-Rep的计算三维物体间距离的方法,即利用物体的表面法向矢量直接计算三维物体间的定向距离。
6) steering vector


导向矢量
1.
In view of the DOA of the other signals attained from the weight vector of the algorithm the steering vectors matrix of the interference signals are established.
首先由MVDR算法确定初始权向量;其次根据该权向量与其它用户波达角方向的关系,建立干扰信号的导向矢量矩阵;然后通过正交投影原理,将期望信号的导向矢量投影到干扰信号的零空间上,从而求得最优权值。
2.
Within the null space of the steering vectors vectors matrix of interference signals, the weight vector which is closest to the steering vector of the expected signal and deeply depresses the interference signals simultaneously comed be obtained with least square method through the linear combination of orthogonal basis.
提出了一种新的用于智能天线中极大抑制干扰的波束形成算法 ,在干扰信号的导向矢量矩阵的零空间内 ,经过正交基矢量的线性组合 ,用最小二乘法求得最接近期望信号导向矢量、并同时对各个干扰信号零陷的权值 。
3.
On the basis of analysis of constraint equations,the actual space-time steering vectors of the desired signal can be solved using the Lagrange multiplier methodology.
该算法在宽带信号模型基础上,分解空时宽带波束形成的约束方程,针对多频点约束,推导出空时二维导向矢量真值,得到空时结构可变对角加载波束形成算法的最优权矢量,并给出加载量求解方程,准确地计算出空时波束形成器的对角加载量。
补充资料:向量
| 向量 vector 一种既有大小又有方向的量。又称矢量。在理论和实际中均广泛应用。速度、加速度、力等都是向量。 从空间中任一点出发,作一直线l,在l上取一点B,则有向线段AB就代表一个向量,记作AB或a(图1),它的大小是线段AB的长度,也称为模或绝对值,记作|a|=a,方向就是l的方向。如果另有A¢B ¢||蜛B,且指向相同,长度相等 ,就说向量AB=A¢B ¢。这种起点可以自由改变的向量常称为自由向量,当点B与A重合时,称为零向量,记作0,它的模为0,方向不确定。模为1的向量称为单位向量,向量a=b,当且仅当它们的方向相同且模相等,非零向量a与b平行或重合记为a∥b。-a是指与a方向相反模相等的向量。a与b垂直,如果它们所在直线垂直,记为a⊥b,除上面这种几何表示法以外,还常用代数方法表示向量,这种方法便于运算,便于进行有关性质的讨论。具体做法如下:在空间取定一右手坐标系(图2),把给定向量的起点放在原点,其终点为P,则a=OP,设P点在坐标系下的坐标为(x,y,z),则a={x,y,z}就是向量a的代数表示,分别称x,y,z为向量a在x轴、y轴、z轴上的分量,零向量o的三个分量均为0,即o={0,0,0}。下面介绍向量的数乘、加减法、内积、外积和混合积等运算。这些运算在代数表示法下简单明了,在几何表示法下直观,各有长处。数乘:向量a与数c相乘,得到向量ca,其模为|ca|=|c||a|,当c>0时,方向与a相同,c<0时,方向与a相反,c=0时,方向不定,得到零向量。若用代数表示法,a={x,y,z},则 ca={cx,cy,cz}。数乘满足结合律:b(ca)=(bc)a。加法:将a=OA,b=OB取在同一起点O(图3),再以OA,OB为边作平行四边形OACB,定义向量OC=c为向量a与b之和。为用代数表示法,a={x1,y1,z1},b={x2,y2,z2},则定义a+b={x1+x2,y1+y2,z1+z2},向量加法满足交换律、结合律和对数乘的分配律。向量的减法可作为加法的逆运算来定义。向量的内积(也称为点积):设a,b均不为零向量,它们的夹角为θ,则定义a·b=|a||b|cosθ,如a、b中有一个为零向量,则定义a·b=0。用代数表示法,当a={x1,y1,z1},b={x2,y2,z2}时,a·b=x1x2+y1y2+z1z2,内积满足交换律、结合律及与数乘的分配律。向量的外积:对于两个不平行的非零向量a、b,定义a×b为向量c,|c|=|a||b||sinθ|,其中θ为a与b的夹角,且c与a、b均垂直,a、b、c的指向构成右手系(图4),因为a×b仍为向量,故外积也称为向量积。用代数表示法时,a×b=c={y1z2-z1y2,z1x2-x1z2,x1y2-y1x2},其中a={x1,y1,z1} ,b={x2,y2,z2},向量的内积与外积间满足关系:(a×b)2=a2b2-(a·b)2 。向量的混合积(a×b)·c ,也记为(a,b,c)。设a={x1,y1,z1},b={x2,y2,z2},c={x3,y3,z3},则 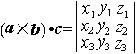
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |