1) assemblage
[英][ə'semblɪdʒ] [美][ə'sɛmblɪdʒ]


系综(统计力学)
2) statistical ensemble


统计系综
1.
The statistical ensemble is usually introduced when the macroscopic nature of body are researched in statistical method.
用统计的方法去研究物体的宏观性质,常引入统计系综。
3) power system analysis software package(PSASP)


电力系统综合计算程序
4) Comprehensive Ability of the Auditing System


审计系统综合能力
5) statistical mechanics


统计力学
1.
Statistical Mechanics for Finite Systems and Temperature Fluctuations;


有限体系统计力学及其温度涨落研究
2.
In this paper, JRG-Fourth statistical mechanics was used to study on the relations between the latex diameter distribution in the emulsion polymerization and the sol stability and gel mechanism property.
采用JRG第四统计力学理论来考察乳液聚合中乳胶粒径分布与聚合物溶胶稳定性、凝胶力学性能之间的关系,找到了在粒径增加过程中乳胶粒微观结构变化的依据,并发现了这种微观结构的变化对聚合物溶胶、凝胶性能产生重要的影响。
3.
The hydrogen and oxygen bridge functions were applied in 3d RISM HNC based on the integral equation theory of statistical mechanics, which was used to improve the calculations of thermodynamic properties of polar and non polar solutions.
把氢 -桥函数和氧 -桥函数应用于统计力学积分方程理论的三维的参考作用点 -超链模型 ( 3d RISM HNC)中 ,用以改进极性和非极性溶质的水溶液的热力学性质的计算 。
6) statistic mechanics


统计力学
1.
According to statistic mechanics research scheme,the crushing statistic mechanics formulae are calculated for mono-size ball size and mixed ball size,respectively.
仿照统计力学研究的科学方法,推导了单一球径球组和混合球径球组破碎的统计力学公式,其最大破碎事件量所对应的球径或配比可作为最佳球径或最佳配比的依据。
补充资料:系综
| 系综 ensemble 在一定的宏观条件下,大量性质和结构完全相同的、处于各种运动状态的、各自独立的系统的集合。全称为统计系综。系综是用统计方法描述热力学系统的统计规律性时引入的一个基本概念;系综是统计理论的一种表述方式;系综并不是实际的物体,构成系综的系统才是实际物体。 研究气体热运动性质和规律的早期统计理论是气体动理论。统计物理学的研究对象和研究方法与气体动理论有许多共同之处,为了避免气体动理论研究中的困难,它不是以分子而是以由大量分子组成的整个热力学系统为统计的个体。系综理论使统计物理成为普遍的微观统计理论。 系统的一种可能的运动状态,可用相宇中的一个相点表示,随着时间的推移,系统的运动状态改变了,相应的相点在相宇中运动,描绘出一条轨迹,由大量系统构成的系综则可表为相宇中大量相点的集合,随着时间的推移,各个相点分别沿各自的轨迹运动,类似于流体的流动。 若系统具有s个自由度,则相宇是以s个广义坐标p(详写为p1、p2……ps)和s个广义动量q(详写为q1、q2……qs)为直角坐标构成的2s维空间。在相宇内任一点(p,q)附近单位相体积元内的相点数目D(p,q,t)称为密度函数。D(p,q,t)在整个相宇的积分等于全部相点数,即等于系综所包含的全部系统数N,与时间t无关。定义ρ(p,q,t)= 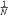 D(p,q,t),称为系综的概率密度函数。ρ(p,q,t)dp dq表示在t时刻出现在(p,q)点附近相体积元dp dq内的相点数在全部相点数中所占的百分数,即表示任一系统在t时刻其运动状态处于(p,q)附近的相体积元dp dq内的概率。显然 ,概率密度函数ρ(p,q,t)满足归一化条件 D(p,q,t),称为系综的概率密度函数。ρ(p,q,t)dp dq表示在t时刻出现在(p,q)点附近相体积元dp dq内的相点数在全部相点数中所占的百分数,即表示任一系统在t时刻其运动状态处于(p,q)附近的相体积元dp dq内的概率。显然 ,概率密度函数ρ(p,q,t)满足归一化条件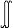 ρ(p,q,t)dpdq=1。 ρ(p,q,t)dpdq=1。统计物理学的基本假设是,系统每一种可能的微观运动状态的概率相等 ,系统的任意宏观量(t)是相应微观量L(p,q)在一定宏观条件下对系统一切可能的微观运动状态的统计平均值,即I(t)= 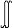 L(p,q)ρ(p,q,t)dp dq。由此可见,经典统计物理的基本课题是确定各种条件下系综的概率密度函数ρ(p,q,t),ρ确定后,即可对相应的热力学系统的宏观性质作出统计描述。这就是统计系综的方法。 L(p,q)ρ(p,q,t)dp dq。由此可见,经典统计物理的基本课题是确定各种条件下系综的概率密度函数ρ(p,q,t),ρ确定后,即可对相应的热力学系统的宏观性质作出统计描述。这就是统计系综的方法。ρ(p,q,t)的具体形式与系统所处的宏观状态有关。如果系统处于平衡态,则 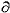 ρ/ ρ/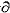 t=0,ρ=ρ(p,q)不显含时间t,在平衡态的系综理论中,由能量和粒子数都固定的系统构成的统计系综称为微正则系综;由与温度恒定的大热源接触,具有确定粒子数和体积的系统构成的统计系综称为正则系综;由与温度恒定的大热源和化学势恒定的大粒子源接触,具有确定体积的系统构成的统计系综称为巨正则系综;由与温度恒定的大热源接触并通过无摩擦的活塞与恒压强源接触,具有确定粒子数的系统构成的统计系综称为等温等压系综。上述各种统计系综都有各自的概率密度函数。 t=0,ρ=ρ(p,q)不显含时间t,在平衡态的系综理论中,由能量和粒子数都固定的系统构成的统计系综称为微正则系综;由与温度恒定的大热源接触,具有确定粒子数和体积的系统构成的统计系综称为正则系综;由与温度恒定的大热源和化学势恒定的大粒子源接触,具有确定体积的系统构成的统计系综称为巨正则系综;由与温度恒定的大热源接触并通过无摩擦的活塞与恒压强源接触,具有确定粒子数的系统构成的统计系综称为等温等压系综。上述各种统计系综都有各自的概率密度函数。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条