1) differential
[英][,dɪfə'renʃl] [美]['dɪfə'rɛnʃəl]


(示)差的,鉴别的;微分;微分的
2) differential
[英][,dɪfə'renʃl] [美]['dɪfə'rɛnʃəl]


微分(的),差动的,差示的
3) differential
[英][,dɪfə'renʃl] [美]['dɪfə'rɛnʃəl]


差别的,差动,微分,差动的,差作用的,差示的,差动装置;差速器
4) nondifferential


无差别的,不可微分的
5) differential
[英][,dɪfə'renʃl] [美]['dɪfə'rɛnʃəl]


微分差动的
补充资料:微分
| 微分 differential 数学基本概念之一。如果函数y=f(x)在x点的增量Δy=f(x+Δx)-f(x)能表为Δy=A·Δx+0(Δx) ,其中A是一个与Δx无关的数,第二项0(Δx)表示当Δx→0时比 Δx高阶的无穷小量,即0(Δx)趋于0的速度比Δx趋于0的速度要快,则称A·Δx为f在x点的微分,记为dy或df(x),并说函数在x点可微。因为自变量x的微分dx=Δx,所以又常把A·Δx记为A·dx。由0(Δx)的意义可知,Δy≈dy。比如半径为r的圆面积S=πr2,若半径增大Δr,则面积增量(即圆环面积)ΔS=π(r+Δr) 2-πr2=2πr·Δr+π(Δr) 2。显然,当Δr→0时,π(Δr) 2趋于0的速度比Δr趋于0的速度要快得多,因此ΔS≈2πr·Δr=dS。它的几何意义是:圆环面积近似等于2πr·Δr。取r=1,Δr=0.01,则ΔS=2π·10-2+π·10-4≈2π·10-2。这样做的好处是与线性函数(即一次函数)有类似的方便,能简单地计算Δy的近似值。也正是因为dy在形上为Δx的线性函数,又是函数增量Δy的主要部分,所以函数在x点的微分dy是Δy的线性主部。 函数y=f(x)在x点可微的充要条件是它在x点有导数y′=f(x),而且dy=f′(x)·dx。因此函数在x点可导与可微是一致的,不必严格区分,有时也把求导运算说成是进行微分运算。 微分在近似计算中有重要作用。它是估计函数增量的有力工具。例如,y=sinx的微分dy=cosx·dx,所以从Δy≈dy知,当|Δx|很小时,sin(x+Δx)≈sinx+cosx·Δx。为求sin31°的近似值,可取x=30°= 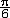 ,Δx=1°= ,Δx=1°=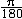 ≈0.01745,得到sin31°≈sin ≈0.01745,得到sin31°≈sin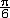 +cos +cos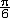 · ·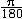 =0.5+ =0.5+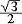 ×0.01745≈0.5151。特别地,若取x=0,记h=Δx,则有sinh≈h。 ×0.01745≈0.5151。特别地,若取x=0,记h=Δx,则有sinh≈h。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条