1) vector
[英]['vektə(r)] [美]['vɛktɚ]


向量(一种容器,有点类似array)
2) vector
[英]['vektə(r)] [美]['vɛktɚ]


向量(一种容器,有点类似array)向量、矢量(看场合)
3) first category vessel


一类容器
4) vector vessel


向量容器
5) A point of reference from which measurements can be made.


一种测量参考点。
6) the first class pressure vessel


一类压力容器
1.
By use of half pipe jacket structure, some vessels identified originally as the first class pressure vessel can be treated as non-pressurized vessels.
压力容器从设计、制造、运行管理都受国家劳动部门的严格管理 ,而使用半圆管夹套 ,可将所述一类压力容器可按常压容器对待。
补充资料:向量
| 向量 vector 一种既有大小又有方向的量。又称矢量。在理论和实际中均广泛应用。速度、加速度、力等都是向量。 从空间中任一点出发,作一直线l,在l上取一点B,则有向线段AB就代表一个向量,记作AB或a(图1),它的大小是线段AB的长度,也称为模或绝对值,记作|a|=a,方向就是l的方向。如果另有A¢B ¢||蜛B,且指向相同,长度相等 ,就说向量AB=A¢B ¢。这种起点可以自由改变的向量常称为自由向量,当点B与A重合时,称为零向量,记作0,它的模为0,方向不确定。模为1的向量称为单位向量,向量a=b,当且仅当它们的方向相同且模相等,非零向量a与b平行或重合记为a∥b。-a是指与a方向相反模相等的向量。a与b垂直,如果它们所在直线垂直,记为a⊥b,除上面这种几何表示法以外,还常用代数方法表示向量,这种方法便于运算,便于进行有关性质的讨论。具体做法如下:在空间取定一右手坐标系(图2),把给定向量的起点放在原点,其终点为P,则a=OP,设P点在坐标系下的坐标为(x,y,z),则a={x,y,z}就是向量a的代数表示,分别称x,y,z为向量a在x轴、y轴、z轴上的分量,零向量o的三个分量均为0,即o={0,0,0}。下面介绍向量的数乘、加减法、内积、外积和混合积等运算。这些运算在代数表示法下简单明了,在几何表示法下直观,各有长处。数乘:向量a与数c相乘,得到向量ca,其模为|ca|=|c||a|,当c>0时,方向与a相同,c<0时,方向与a相反,c=0时,方向不定,得到零向量。若用代数表示法,a={x,y,z},则 ca={cx,cy,cz}。数乘满足结合律:b(ca)=(bc)a。加法:将a=OA,b=OB取在同一起点O(图3),再以OA,OB为边作平行四边形OACB,定义向量OC=c为向量a与b之和。为用代数表示法,a={x1,y1,z1},b={x2,y2,z2},则定义a+b={x1+x2,y1+y2,z1+z2},向量加法满足交换律、结合律和对数乘的分配律。向量的减法可作为加法的逆运算来定义。向量的内积(也称为点积):设a,b均不为零向量,它们的夹角为θ,则定义a·b=|a||b|cosθ,如a、b中有一个为零向量,则定义a·b=0。用代数表示法,当a={x1,y1,z1},b={x2,y2,z2}时,a·b=x1x2+y1y2+z1z2,内积满足交换律、结合律及与数乘的分配律。向量的外积:对于两个不平行的非零向量a、b,定义a×b为向量c,|c|=|a||b||sinθ|,其中θ为a与b的夹角,且c与a、b均垂直,a、b、c的指向构成右手系(图4),因为a×b仍为向量,故外积也称为向量积。用代数表示法时,a×b=c={y1z2-z1y2,z1x2-x1z2,x1y2-y1x2},其中a={x1,y1,z1} ,b={x2,y2,z2},向量的内积与外积间满足关系:(a×b)2=a2b2-(a·b)2 。向量的混合积(a×b)·c ,也记为(a,b,c)。设a={x1,y1,z1},b={x2,y2,z2},c={x3,y3,z3},则 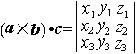
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |