1) support of distribution
广义函数支集
2) supports of distribations
广义函数的支集
3) generalized support function
广义支持函数
1.
By means of the part intersection,the generalized support function and the restricted chord function and the combination with the simple maths and the related theory of measure,the individual expressions for the kinematic measure of ellipse and its properties have been derived.
运用“部分相交法”及广义支持函数,限弦函数,交体等概念结合初等数学及测度的相关理论,推导出椭圆的包含测度的具体表达式及相关的性质。
2.
By using the generalized support function,we reckon the mean distance of two points of circle,rectangle and ellipse,and deduct the idiographic process.
本文研究了凸域内两点间的平均距离公式,利用广义支持函数的方法分别求出了圆、矩形、椭圆域内两点间的平均距离,并给出了具体的求解过程。
3.
Ren Delin introduced the notion of generalized support function and restricted chord function of a convex body in the plane and used them to establish integral formulas for the containment measure of a line segment inside a convex body.
本文研究了凸域内定长线段的包含测度问题,利用广义支持函数和限弦函数,得到了一类特殊凸域的包含测度。
4) the generalized support function
广义支持函数
1.
Using a universal formula for the mean length of a convex set and the generalized support function,this paper has arrived at the mean length of the ellipse.
主要利用广义支持函数和凸域内弦的平均长度的一个普遍公式,得到椭圆域内弦的平均长度,并对矩形域内弦的平均长度的极值作了研究,得出当为正方形域时,弦的平均长度最大。
2.
By using the generalized support function,we can get the integral for the power of chords of a convex set.
通过广义支持函数与凸域的弦幂积分,建立了凸域内弦的平均长度的一般公式,并用此公式得出了圆域和矩形域内弦的平均长度。
5) generalized convex set functions
广义凸集函数
1.
The paper presents necessary and sufficient conditions for solutions to multiobjectivematheamatical programming with generalized convex set functions which popularized the documents ″Suffi-cient and necessary conditions for solutions to multiobjective mathematical programming with generalized con-vex set functions″and etc.
给出了广义凸集函数多目标数学规划解的充分必要条件，它是对多目标广义凸规划解的充分必要条件等文献的推
6) function general convexity
广义凸n集函数
补充资料：广义函数
| 广义函数 generalized function，distribution 古典函数概念的推广。关于广义函数的研究构成了泛函分析中有着广泛应用的一个重要分支。历史上第一个广义函数是由物理学家P.A.M.狄拉克引进的，他因为陈述量子力学中某些量的关系时需要引入了“函数”δ（x）：当x≠0时，δ（x）＝0，但 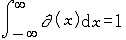 。按20世纪前所形成的数学概念是无法理解这样奇怪的函数的。然而物理学上一切点量，如点质量、点电荷、偶极子、瞬时打击力、瞬时源等物理量用它来描述不仅方便、物理含义清楚，而且当它被当作普通函数参加运算，如对它进行微分和傅里叶变换，将它参与微分方程求解等所得到的数学结论和物理结论是吻合的。这就迫使人们要为这类怪函数确立严格的数学基础。最初理解的方式之一是把这种怪函数设想成直线上某种分布所相应的“密度”函数。所以广义函数又称为分布，广义函数论又称分布理论。用分布的观念为这些怪函数建立基础虽然很直观，但对于复杂情况就又显得繁琐而不很明确。后来随着泛函分析的发展，L.施瓦尔茨（1945）用泛函分析观点为广义函数建立了一整套严格的理论，接着I.M.盖尔范德对广义函数论又作了重要发展。从此，广义函数被广泛地应用于数学、物理、力学以及分析数学的其他各个分支，例如微分方程、随机过程、流形理论等等，它还被应用到群的表示理论，特别是它有力地促进了偏微分方程近30年来的发展。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条