1) Calculus of Variations & Tensor


变分法与张量
2) tensor analysis method


张量分析法
1.
The equations in terrain following coordinate system with hydrostatic hypothesis deduced by using a general method are compared with the equations deduced by using tensor analysis method.
通过比较常用地形σ坐标的流体静力中尺度大气控制方程的一般导出与利用张量分析法的导出,分析了前者只限用于很小地形坡度的原因。
3) The rotating transform tensor


旋转变量张量法
5) component of extension deformation


扩张变形分量
6) Three-way data resolution methods


张量分辨算法
补充资料:变分法
| 变分法 calculus of variations 研究泛函的极值的方法。泛函就是函数的函数,给定一个函数集合Y,若对Y中的每一函数y按某一确定的规则J有一确定的实数J [y] 与之对应,就说在集合Y上给定了一个泛函J。若泛函J在Y中的y0处取的值J[y0]是J在Y中所有的y 处所取值J [y]中的最大(小)的一个 ,则说J [ y0]是最大(小)值,y0称为最大(小)值函数。设Y′是Y中在 y0附近的函数组成的子集,若J[ y0 ]是J 在Y′上取的最大(小)值,则称J[y0 ]是极大(小)值,而y0称为极大(小)值函数。极大(小)值统称极值,极大值函数和极小值函数统称极值函数。变分法的核心问题就是求泛函的极值函数和相应的极值。
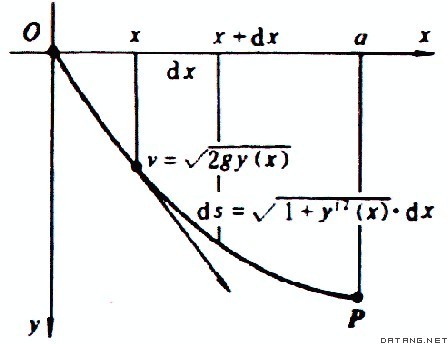
变分法的第一个著名例子是最速降曲线问题,它是由约翰第一·伯努利在1696年以挑战的口吻向当时的数学家提出的。设O和P是铅直平面 xO y内高度不同的两点,一质点在重力作用下从O点沿一曲线滑落到P点,假定无摩擦和其他阻力,问曲线呈何形状时其滑落的时间最短?设滑落曲线方程为y=y(x),由能量守恒定律和弧长公式可知所需时间为 
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
||
| ©2011 dictall.com | ||