1) sieve method


筛法,逐步淘汰法
2) successive sweep method


逐步淘汰法
4) phase out


使逐步淘汰
5) elimination strategy


淘汰法
1.
SVM group incorporated with the elimination strategy is proposed to deal with the multi-class face recognition problem.
由于支持向量机本身是一个两类问题的判别方法 ,在处理多类问题时 ,提出了一种基于支持向量机组的淘汰法 ,这种方法考虑到了各判别函数的 VC置信范围的差异 ,同时利用判别函数间的冗余来降低识别误差 。
6) elimination algorithm


淘汰算法
1.
This paper mainly discusses a assumption of account page faults,which transformation from LRU and LFU elimination algorithm.
本文主要讨论一种从LRU与LFU淘汰算法中变形得到的一种求缺页中断的设想。
补充资料:筛法
| 筛法 sieve method 在数论中有广泛应用的一个初等数学方法。起源于古老的埃拉托斯特尼筛法,这个古老筛法是选出不超过N的素数表的方法,它基于下述一个简单结果如果n≤N, 且n是复合数,则n必为一个不大于 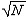 的素数所整除 ,具体做法如下:先列出不大于 的素数所整除 ,具体做法如下:先列出不大于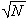 的全体素数 ,记为 2=p1<p2<…<pr≤ 的全体素数 ,记为 2=p1<p2<…<pr≤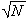 ,然后依次写出整数2,3,4,…,N,在其中留下p1=2,然后把p1的倍数全划掉,再留下p2=3,而把p2的倍数全划掉,继续如此往下做 ,直到最后留下pr,而把pr的倍数全划掉,最后所留下的整数就是不超过N的全体素数。埃拉托斯特尼筛法的改进和发展,成为近代解析数论的重要工具。例如V.布龙在 1920年对上述古老筛法做了重要改进,证明了命题(9,9)。这里命题(a,b )表示每个足够大的偶数都可以表成两个正奇数之和,而这二个奇数所含素因子个数分别不超过a和b,这是对哥德巴赫猜想研究的重要贡献。他的方法称为布龙筛法。以后筛法又得到进一步改进,相继提出所谓罗塞筛法,塞尔伯格筛法和大筛法等。 ,然后依次写出整数2,3,4,…,N,在其中留下p1=2,然后把p1的倍数全划掉,再留下p2=3,而把p2的倍数全划掉,继续如此往下做 ,直到最后留下pr,而把pr的倍数全划掉,最后所留下的整数就是不超过N的全体素数。埃拉托斯特尼筛法的改进和发展,成为近代解析数论的重要工具。例如V.布龙在 1920年对上述古老筛法做了重要改进,证明了命题(9,9)。这里命题(a,b )表示每个足够大的偶数都可以表成两个正奇数之和,而这二个奇数所含素因子个数分别不超过a和b,这是对哥德巴赫猜想研究的重要贡献。他的方法称为布龙筛法。以后筛法又得到进一步改进,相继提出所谓罗塞筛法,塞尔伯格筛法和大筛法等。中国的数学家对筛法的理论和应用有重要贡献。1957年王元证明了命题(2,3),1962年潘承洞证明了命题(1,5),1966年陈景润证明了命题(1,2),陈景润的详细证明在1973年发表后,世界公认这是筛法理论的最卓越的应用成果。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条