1) integration
[英][,ɪntɪ'ɡreɪʃn] [美]['ɪntə'greʃən]


积分;集成,集合;综合;积累,累计
2) integration
[英][,ɪntɪ'ɡreɪʃn] [美]['ɪntə'greʃən]


集成;结合;综合;整体化;积分;求积;积累
3) comprehensive accumulation


综合积累
4) come together;assemble or accumulate;gather


聚集;召集;积累;集合;齐集
5) dynamic accumulation


合成积累
1.
Study on the relation between the dynamic accumulation of secondary metabolites and the phenological period of Eucommia ulmoides Oliv.;
杜仲次生代谢物合成积累与物候期的研究
6) integrated
[英]['ɪntɪɡreɪtɪd] [美]['ɪntə'gretɪd]


集成的;积分的;累积的
补充资料:积分
| 积分 integral 从不同的问题抽象出来的两个数学概念。定积分和不定积分的统称。不定积分是为解决求导和微分的逆运算而提出的。例如:已知定义在区间I上的函数f(x),求一条曲线y=F(x),x∈I,使得它在每一点的切线斜率为F′(x)= f(x)。函数f(x)的不定积分是f(x)的全体原函数(见原函数),记作 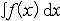 。如果F(x)是f(x)的一个原函数,则 。如果F(x)是f(x)的一个原函数,则 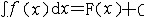 ,其中C为任意常数。例如, ,其中C为任意常数。例如,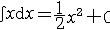 定积分是以平面图形的面积问题引出的。如右上图,y=f(x)为定义在[a,b]上的函数,为求由x=a,x=b ,y=0和y=f(x)所围图形的面积S,采用古希腊人的穷竭法,先在小范围内以直代曲,求出S的近似值,再取极限得到所求面积S,为此,先将[a,b]分成n等分:a=x0<x1<…<xn=b,取ζi∈[xi-1,xi],记Δxi=xi-xi-1, 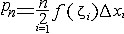 ,则pn为S的近似值,当n→+∞时,pn的极限应可作为面积S。把这一类问题的思想方法抽象出来,便得定积分的概念:对于定义在[a,b]上的函数y=f(x),作分划a=x0<x1<…<xn=b,若存在一个与分划及ζi∈[xi-1,xi]的取法都无关的常数I,使得 ,则pn为S的近似值,当n→+∞时,pn的极限应可作为面积S。把这一类问题的思想方法抽象出来,便得定积分的概念:对于定义在[a,b]上的函数y=f(x),作分划a=x0<x1<…<xn=b,若存在一个与分划及ζi∈[xi-1,xi]的取法都无关的常数I,使得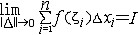 ,其中 ,其中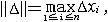 则称I为f(x)在[a,b]上的定积分,表为 则称I为f(x)在[a,b]上的定积分,表为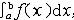 即 即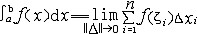 称[a,b]为积分区间,f(x)为被积函数,a,b分别称为积分的上限和下限。当f(x)的原函数存在时,定积分的计算可转化为求f(x)的不定积分: 称[a,b]为积分区间,f(x)为被积函数,a,b分别称为积分的上限和下限。当f(x)的原函数存在时,定积分的计算可转化为求f(x)的不定积分: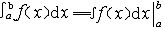 这是牛顿莱布尼兹公式。例如, 这是牛顿莱布尼兹公式。例如,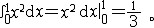
|
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条