1) derivative
[英][dɪ'rɪvətɪv] [美][də'rɪvətɪv]


导数;变形;衍生物
2) derivative
[英][dɪ'rɪvətɪv] [美][də'rɪvətɪv]


导数,衍生物,变形,派生的
3) deriv.derivative


衍生物,导数(数)
4) derivate
[英]['deriveit] [美]['dɛrə,vet]


导数,微商;衍生物
5) fissionable derivative


可裂变衍生物
补充资料:导数
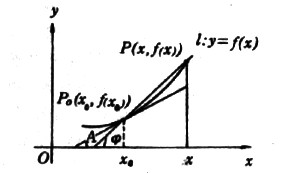
| 导数 derivative 由速度问题和切线问题抽象出来的数学概念。又称变化率。如一辆汽车在10小时内走了 600千米,它的平均速度是60千米/小时,但在实际行驶过程中,是有快慢变化的,不都是60千米/小时。为了较好地反映汽车在行驶过程中的快慢变化情况,可以缩短时间间隔,设汽车所在位置x与时间t的关系为x=f(t),那么汽车在由时刻t0变到t1这段时间内的平均速度是 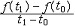 ,当 t1与t0很接近时,汽车行驶的快慢变化就不会很大,平均速度就能较好地反映汽车在t0 到 t1这段时间内的运动变化情况 ,自然就把极限 ,当 t1与t0很接近时,汽车行驶的快慢变化就不会很大,平均速度就能较好地反映汽车在t0 到 t1这段时间内的运动变化情况 ,自然就把极限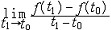 作为汽车在时刻t0的瞬时速度,这就是通常所说的速度。一般地,假设一元函数 y=f(x )在 x0点的附近(x0-a ,x0 +a)内有定义,当自变量的增量Δx= x-x0→0时函数增量 Δy=f(x)- f(x0)与自变量增量之比 作为汽车在时刻t0的瞬时速度,这就是通常所说的速度。一般地,假设一元函数 y=f(x )在 x0点的附近(x0-a ,x0 +a)内有定义,当自变量的增量Δx= x-x0→0时函数增量 Δy=f(x)- f(x0)与自变量增量之比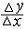 的极限 的极限 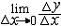 存在且有限,就说函数f在x0点可导,记作 存在且有限,就说函数f在x0点可导,记作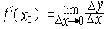 ,称之为f在x0点的导数(或变化率)。若函数f在区间I 的每一点都可导,便得到一个以I为定义域的新函数,记作 f′,称之为f的导函数,简称为导数。函数y=f(x)在x0点的导数f′(x0)的几何意义: ,称之为f在x0点的导数(或变化率)。若函数f在区间I 的每一点都可导,便得到一个以I为定义域的新函数,记作 f′,称之为f的导函数,简称为导数。函数y=f(x)在x0点的导数f′(x0)的几何意义: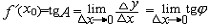 ,表示曲线l 在P0[x0,f(x0)] 点的切线斜率。 ,表示曲线l 在P0[x0,f(x0)] 点的切线斜率。
|
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条