1) complex
[英]['kɔmpleks] [美][kəm'plɛks, 'kɑm,plɛks]
复数，复量;复合的，合成的，配合的，络合的，复杂的;集合体，综合体;络合物，配合物;联合企业;全套装置;(数学上的)线丛，子集
2) complex
[英]['kɔmpleks] [美][kəm'plɛks, 'kɑm,plɛks]
合成的;复杂的;合成物;集合体
3) complex
[英]['kɔmpleks] [美][kəm'plɛks, 'kɑm,plɛks]
复杂的;合成的,综合的 n.联合体
4) composition of set
集合的复合
5) composite
[英]['kɔmpəzɪt] [美][kəm'pɑzət]
混合成的，综合成的n.合成物，复合材料
6) compound
[英]['kɔmpaund] [美][kɑm'paＵnd]
混合物,[化]化合物 复合的,混合,配合
补充资料：复数
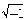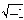| 复数 complex number 形如a＋bi的数。式中a，b 为实数，i是 一个满足i2＝－1的数，因为任何实数的平方不等于－1，所以i不是实数，而是实数以外的新的数。在复数a＋bi中，a 称为复数的实部，b称为复数的虚部，i称为虚数单位。当虚部等于零时，这个复数就是实数；当虚部不等于零时，这个复数称为虚数，虚数的实部如果等于零，则称为纯虚数。由上可知，复数集包含了实数集，因而是实数集的扩张。 复数的产生来自解代数方程的需要。16世纪，意大利数学家G.卡尔达诺首先用公式表示出了一元三次方程的根，但公式中引用了负数开方的形式，并把i＝  当作数，与其他数一起参与运算。由于人们无法理解 的实质，所以在很长时间内不承认负数的平方根也是数，而称之为虚数。直到19世纪，数学家们对这些虚数参与实数的代数运算作出了科学的解释，并在解方程和其他领域中使虚数得到了广泛的应用，人们才认识了这种新的数。复数的四则运算规定为： （a＋bi）＋（c＋di）＝（a＋c）＋（b＋d）i， （a＋bi）－（c＋di）＝（a－c）＋（b－d）i， （a＋bi）·（c＋di）＝（ac－bd）＋（bc＋ad）i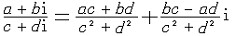，  （c与d不同时为零）。复数有多种表示形式，常用形式z＝a＋bi叫做代数式。此外有下列形式。 ①几何形式。复数z＝a＋bi 用直角坐标平面上点Z（a，b）表示。这种形式使复数的问题可以借助图形来研究。也可反过来用复数的理论解决一些几何问题。 ②向量形式。复数z＝a＋bi用一个以原点O为起点，点Z（a，b）为终点的向量OZ表示。这种形式使复数的加、减法运算得到恰当的几何解释。 ③三角形式。复数z＝a＋bi化为三角形式 z＝｜z｜（cosθ＋isinθ） 说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |