1) mechanogram
['mekənəɡræm]


机械性运动记录图
2) mechanogram
['mekənəɡræm]


机械记录图
3) mechanical record


机械记录
4) kinematic diagram


机械运动简图
5) motion record


运动记录
6) mechanical recording head


机械记录器
补充资料:机械运动
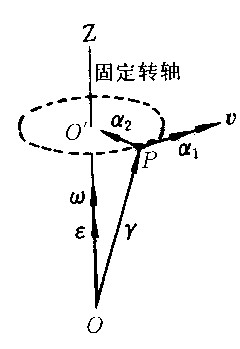
| 机械运动 mechanical motion 物体空间位置随时间的变动。又称力学运动。包括平动、转动、变形、流动、振动、波动、扩散以及它们的复合运动等,平衡或静止,则是其中的一种特殊情况。其他物理运动以及化学的、生命的运动等远比机械运动复杂,但都离不开组成物质的各种粒子的位置变动,可以说都是以粒子的机械运动为基础。因此机械运动是最简单、最基本的运动。物体的机械运动都是相对于另一物体或本物体的某一部分而言,被参考的物体或物体的一部分称为参考物。为描述机械运动还须在参考物上设置坐标系,称参考系。 平动 物体内任意直线在运动过程中始终同起动时的位置保持平行的机械运动。平行移动的简称。做平动的物体必须是体积和形状保持不变的刚体,而且物体内任一点的轨迹、速度和加速度必须完全相同。平动时,刚体内各点的运动相同,其中任一点的运动都可代表整个刚体的运动,因此,刚体的平动又可归结为质点的运动学问题(见直线运动、曲线运动)。内燃机活塞的运动、仿型车床上靠模杆和刀架的运动等都是平动。 转动 通常指刚体转动,又分定轴转动和定点转动两类。 ①定轴转动。运动过程中,刚体内某一直线保持不动的机械运动。这条直线称转轴。刚体内其他各点分别在垂直转轴的各平面内作圆周运动,圆心都在转轴上。定轴转动刚体(例如转动的机器轮)具有一个自由度,可用转角 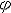 来定位。转角 来定位。转角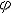 随时间t的变化规律 随时间t的变化规律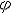 =f(t )称刚体的定轴转动方程。已知定轴转动方程,就能求出各时刻的角速度和角加速度,从而可求出刚体中任一点ρ的速度v和加速度a(图1): =f(t )称刚体的定轴转动方程。已知定轴转动方程,就能求出各时刻的角速度和角加速度,从而可求出刚体中任一点ρ的速度v和加速度a(图1):
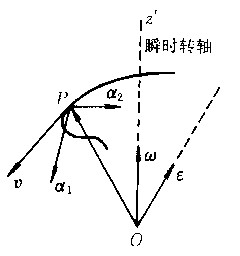
v=ω×γ,a=a1+a2=ε×γ+ω×v ,式中γ为点P的矢径;a1=ε×γ为切向加速度,和速度v共线;a2=ω×v为向心加速度,恒指向圆心O′。 ②定点转动。运动过程中,刚体内某一点保持不动的机械运动。绕定点转动的刚体只有一点不动,其他各点分别在以该固定点为中心的同心球面上运动。每一时刻t,刚体以角速度ω(t)绕穿过该固定点的瞬时转轴转动,而瞬时转轴的位置是随着时间而变的。定点转动刚体(例如陀螺转子)具有3个自由度,通常用欧拉角ψ、θ、 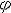 来定位。欧拉角随时间的变化规律ψ=f1(t),θ=f2(t), 来定位。欧拉角随时间的变化规律ψ=f1(t),θ=f2(t),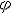 =f3(t)称刚体的定点转动方程。已知定点转动方程,就能求出各时刻的角速度ω(t)和角加速度ε(t),从而可求出定点转动刚体内任一点P的速度v和加速度a(图2): =f3(t)称刚体的定点转动方程。已知定点转动方程,就能求出各时刻的角速度ω(t)和角加速度ε(t),从而可求出定点转动刚体内任一点P的速度v和加速度a(图2):
v=ω×γ,a=a1+a2=ε×γ+ω×υ,式中γ为点P的矢径;a1=ε×γ为转动加速度,沿着(ε,γ)平面的法线方向,一般并不和速度v共线;a2=ω×v为轴向加速度,恒垂直并指向瞬时转轴,但不沿点P轨迹的主法线方向。 变形 物体形状或(和)体积的改变。在外力作用下,或由于温度、湿度等环境因素的改变都会引起物体的变形。其中线段长度的变化称伸长(或缩短)变形,两互相垂直线段所夹直角的变化称为剪切变形。在固体力学中,常通过对变形规律的分析来求变形体各点的应变和应力。 流动 流体的运动。水和空气是两种最常见的流体。具有易流性,无论受到多么小的剪切力,都会连续变形,这是流体区别于固体的一个基本性质。例如,沿Ox轴的纯剪切流动,其速度u=ay,式中a为常数(图3a)。在流体中取正方形微团1234,过一段时间后运动到1′2′3′4′,变成菱形,可以看成是3种运动的复合:①平动。微团1234向右平移使3与3′,4与4′重合(图3b)。②转动。正方形1234微团绕轴3转动,使对角线23与2′3′重合(图3c)。③变形。剪切微团1234,使23伸长与2′3′重合(图3d)。由此可见,即使流线都是直线的简单流动也还是由平动、转动和变形这3种基本运动形式复合而成。因此,流体微团运动和刚体运动的主要差别就在于多了变形速度部分。
振动 力学系统中,质点的位移在其基准值上下交替变化的过程。有单自由度系统(如弹簧振子、钟摆)振动和多自由度系统振动。有限多自由度系统与离散系统相对应,其振动由常微分方程描述,无限多自由度系统与连续系统(如杆、梁、板、壳等)相对应,其振动由偏微分方程描述。 机械波 机械振动在介质中传播所形成的一种运动形式。例如,水面波就是由机械振动在水面的传播而形成的。质点振动方向与振动传播方向互相垂直的波称横波,地震学中也称S波。弦上传播的波就是横波的一个实例。质点振动方向与振动传播方向一致的波称纵波,地震学中也称P波。声波就是在空气中传播的纵波。
|
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条