1) applied nonstandard analysis


应用非标准分析
2) non-standard analysis


非标准分析
1.
The area formula is established under parameter coordinate system by non-standard analysis method.
利用非标准分析(NSA)的方法建立参数坐标下统一面积公式,并以此推导出极坐标下的面积公式,将直角坐标和极坐标下的面积公式统一归纳到参数坐标之下,解决了一般数学分析书中3种坐标系下面积公式不能融合的问题。
2.
MethodsThe method of historical analysis and the viewpoint of non-standard analysis are used to study the original works of Cauchy.
方法 运用历史分析的方法,采用非标准分析的观点对原始文献进行研究。
3.
The applications of LST theorem to the non-standard analysis are discussed.


讨论 LST 定理对非标准分析的应用。
3) nonstandard analysis


非标准分析
1.
By using the method of nonstandard analysis, the paper gives rigorously treatments to three formulae of Delta functions in the book titled "Relativistic Quantum Mechanics" written by James D.
本文采用非标准分析的方法,对J。
2.
Combining the nonstandard analysis,the completeness of the differential test is discussed.
这一判别法简单易推广,结合非标准分析,论述了微分判别法的完备性,同时该方法也是一般的函数项级数和无穷限积分敛散性的判别法。
3.
By using nonstandard analysis, we define new generalized functions as discrete functions, and their derivatives are defined as difference quotients.
在非标准分析框架下 ,用离散函数定义新广义函数 ,用差商定义其导数 。
4) dard strain gauge analyser


标准应变分析器
5) abnormal application analysis


非常规应用分析
6) applied nonlinear analysis


应用非线性分析
补充资料:非标准分析
| 非标准分析 non-standard analysis 数学中利用现代数理逻辑把通常实数结构扩张为包括无穷小数与无穷大数的结构而形成的一个新分支。美国数理逻辑学家A.鲁宾逊于1960年创立。鲁宾逊证明,实数结构R可扩张为包含无穷小数和无穷大数的结构R*,在一定意义下R*与R有相同的性质。称R*中的数为超实数,形象地说,是在普通实数中又加进了无穷小数(其绝对值小于任何实数)及无穷大数(其绝对值大于任何实数)。当两个超实数α与β相差为无穷小时,就称α无限接近于β,记为α 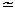 β ,这是一个等价关系。每个关于这个等价关系的等价类包含唯一的标准实数a。称a所在的等价类μ( a)为一个单子,单子不是R*中的数,而相当于R中的数,超实数可以进行四则运算,满足通常的运算规律,也可以有大小顺序。由此标准分析里的许多概念、定理等可以自然地扩张到非标准分析中。如区间〔a,b〕扩张为〔a,b〕*,R中的函数扩张为f(x)*,函数f(x)在标准点x0连续可定义为x β ,这是一个等价关系。每个关于这个等价关系的等价类包含唯一的标准实数a。称a所在的等价类μ( a)为一个单子,单子不是R*中的数,而相当于R中的数,超实数可以进行四则运算,满足通常的运算规律,也可以有大小顺序。由此标准分析里的许多概念、定理等可以自然地扩张到非标准分析中。如区间〔a,b〕扩张为〔a,b〕*,R中的函数扩张为f(x)*,函数f(x)在标准点x0连续可定义为x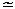 x时,f(x)* x时,f(x)* 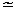 f(x0)*;函数f(x)在〔a,b〕上一致连续可定义为当x′ f(x0)*;函数f(x)在〔a,b〕上一致连续可定义为当x′ x″,x′,x″∈〔a,b〕*时f(x′)*≈f(x″)*。像这样在R上展开的数学分析理论称为非标准分析,通常的数学分析则称为标准分析。 x″,x′,x″∈〔a,b〕*时f(x′)*≈f(x″)*。像这样在R上展开的数学分析理论称为非标准分析,通常的数学分析则称为标准分析。非标准分析的一个重要定理是转换定理:每个关于R可形式化的命题,如果对R成立,则经过适当解释(即把R中的对象解释为R*中相应的对象 )对R*也成立,反之亦然。因此也可以说,利用R和R*互相转换来研究数学分析的方法,称为非标准分析。 非标准分析使无穷小获得新生。在微积分发明的时期,I.牛顿,特别是G.W.莱布尼兹使用无穷小方法,在一阶和高阶无穷小基础上,发展起微积分理论。因它不严格而倍遭非难。A.L.柯西和K.魏尔斯特拉斯等使微积分奠基于极限理论上,数学分析由此臻于严密但失去了无穷小算法的简明与直观。鲁宾逊用数理逻辑方法严谨地论证了无穷小的存在性,重新用它来刻画微积分。这不仅能表现状态,还能表明过程,直观而简洁。非标准分析一经问世便得到迅速发展,并用它解决了许多问题。从方法论上来说,还能将过去一些深刻结果的证明加以简化。 非标准分析发展很快,已有群论、非标准泛函分析等。它有不少应用。凡是对某类数学对象,用类似于上述的扩张来研究的都可称为非标准分析。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条