1) pauli approximation


泡利近似
2) Rayleigh approximation


瑞利近似
4) Rytov approximation


利托夫近似
5) Hartree-Fock approximation


哈特利-福克近似
6) Hartree approxima-tion method


含时哈特利近似方法
补充资料:泡利
| 泡利(1900~1958) Pauli,Wolfgang Ernst 瑞士籍奥地利物理学家。1900年4月25日生于维也纳,1958年12月15日卒于苏黎世 。1918年中学毕业后就成为慕尼黑大学的研究生 ,1921年获博士学位后,赴格丁根大学随M.玻恩研究一学期,再赴哥本哈根大学随A.N.玻尔一年。1940年任普林斯顿高级研究院的理论物理访问教授。 1921年 ,泡利20岁时为《数学科学百科全书》写相对论,此书在数学界具权威性。1924年提出说明电子能态的第四个量子数其数值可取作 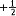 或 或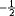 。后来发现,这两个数值代表费米子自旋的两种可能取向。1925年发现不相容原理(今称泡利不相容原理),即一个原子内不能有一个以上电子具有相同的状态。这个原理把量子论和观察到的原子特性联系起来 。为此获1945年诺贝尔物理学奖。在20世纪20年代后期观察到,当一个原子核发射出一个β粒子(电子)时,总有一些能量和动量丧失掉 ,这就违反了守恒律 。泡利在1930年提出,丧失掉的能量和动量是被某种中性粒子(后来由E.费米命名为中微子)从核里带走了。此外,泡利对量子场论也有重大贡献。 。后来发现,这两个数值代表费米子自旋的两种可能取向。1925年发现不相容原理(今称泡利不相容原理),即一个原子内不能有一个以上电子具有相同的状态。这个原理把量子论和观察到的原子特性联系起来 。为此获1945年诺贝尔物理学奖。在20世纪20年代后期观察到,当一个原子核发射出一个β粒子(电子)时,总有一些能量和动量丧失掉 ,这就违反了守恒律 。泡利在1930年提出,丧失掉的能量和动量是被某种中性粒子(后来由E.费米命名为中微子)从核里带走了。此外,泡利对量子场论也有重大贡献。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条