1) aerodynamic focus


气动力学焦点
2) gasdynamic focus


气体动力学焦点
1.
The properties of the gasdynamic focus,formed by shock wave focusing,were analyzed.


对激波聚焦形成的气体动力学焦点的特性进行了分析,结果表明,入射激波在两种反射器反射后聚焦所形成的气体动力学焦点均是由三波点在轴心处的会聚所导致的,气体动力学焦点位于相应的反射器壁面的几何焦点附近。
3) aerodynamic center axis


气动力中心轴;焦点轴
4) kinetics of coking


结焦动力学
6) isokinetic point


等动力学点
1.
The decomposition processes and kinetic parameters of RDX and HMX are markedly affected by test conditions, specimen state and test method, and the "kinetic compensation effect"and "isokinetic points(temperatures)" exist in these parameters.
RDX和HMX在不同的分解阶段有不同的动力学参数和机理函数,其分解过程和动力学参数受试验条件、样品状态和试验方法的影响很大,但这些参数之间存在"动力学补偿效应"和"等动力学点"。
补充资料:传热学:透平机械气体动力学
透平机械气体动力学:
流体动力学的分支之一﹐主要研究透平机械中的气体运动和运动著的气体与透平机械相互作用。透平机械内部有相间排列的动轮和静轮﹐有功的输出或输入﹐气体流道形状复杂。因此﹐研究这类气体运动时必须考虑﹕动轮与静轮内的相对流动和绝对流动﹐以及它们之间的相互关联﹑转换和衔接﹔主流和边界层的相互干涉﹐包括跨音速工况中激波和边界层的相互干涉﹔透平机械特有的边界条件﹐例如週期性条件等。
通常採用柱坐标系 (x﹑y﹑z)来描述透平机械内部的气体流场﹐也就是把速度﹑压力﹑密度和温度等参数视为﹑﹑和时间的函数。若将坐标系与动轮固结在一起﹐坐标系上所观察到的就是工质相对於动轮的运动﹐这种坐标系称为相对坐标系。若将坐标系与地面相固结﹐则称为绝对坐标系。这两种坐标系可以相互转换。
在透平机械内部﹐气体的实际流动非常复杂﹐具有三维和非定常的性质﹐且工质本身又是黏性的可压缩实际气体。描述这种流动的方程有连续方程﹑黏性可压缩气体的运动方程﹑能量方程和实际气体的状态方程等。要準确地求解这类具有 4个自变量的非线性偏微分方程组的初步近似值的问题﹐在数学上尚存在困难。为此﹐必须设法对问题进行合理简化。
20世纪以前﹐透平机械中的气体流动是按照一维流动理论设计计算的。1839年﹐A.J.C.B.de圣维南和L.万策尔第一次导出喷管中可压缩气体的一维等熵流动方程。1894年﹐瑞典工程师拉瓦尔﹐C.G.P.de取得了收缩-扩张喷管(后称拉瓦尔喷管)的专利﹐并将它用於汽轮机。二维流动理论產生於1920年。最初是按孤立机翼理论来设计轴流式压气机(即压缩机)叶片﹐后来又修正了相邻叶片的影响。为提高透平机械性能﹐20世纪初开始发展平面叶栅模型。到20世纪中叶﹐已能计算具有任意形状型线叶栅中的位势流动﹐以及按合理规定的表面压力分布来确定叶片形状。
假设气体在无叶间隙中作轴对称定常流动﹐气体的径向分速为零﹐则可把透平机械中的三维流场人为地分解成无叶间隙中流动参数沿径向的变化和圆柱面内的二维流动。但这种假设具有明显的近似性质﹐对於轮轂比小﹑通道子午扩张角大的透平机械尤为如此。为了使流动模型更接近实际﹐必须发展透平机械的三维流动理论。
1905年﹐H.洛伦茨提出通流理论﹐即无限多叶片理论。这种理论假设叶片数目趋於无限多﹐而叶片厚度趋於无限薄。这样﹐两相邻叶片间的各相对流面的形状与叶片中心面一致﹐且周向变化量趋近於零。实际叶片的作用是通过引入一个假想质量力场的办法来考虑的。这样可求得与叶片中心面相重合的极限流面上的气流的解。50年代初﹐中国科学家吴仲华对通流理论作出改进﹐并提出透平机械三维流动通用理论。这个理论引入S 1和S 2两类相对流面的概念﹐并分别导出了这两类流面流动的基本方程﹐通过这两类流面的适当组合和交替运用﹐就可以把一个实际的三维流动问题分解为两个分别沿著S 1和S 2相对流面的相关的二维流动问题(见图 三维流动通用理论示意图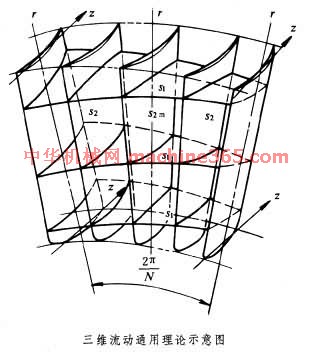 )。实际上﹐通常假定S 1流面是一些任意旋成面﹐而在S 2流面族中只取一个称为S 2m的中心流面。这样可得到三维流动的初步近似。
)。实际上﹐通常假定S 1流面是一些任意旋成面﹐而在S 2流面族中只取一个称为S 2m的中心流面。这样可得到三维流动的初步近似。
流体动力学的分支之一﹐主要研究透平机械中的气体运动和运动著的气体与透平机械相互作用。透平机械内部有相间排列的动轮和静轮﹐有功的输出或输入﹐气体流道形状复杂。因此﹐研究这类气体运动时必须考虑﹕动轮与静轮内的相对流动和绝对流动﹐以及它们之间的相互关联﹑转换和衔接﹔主流和边界层的相互干涉﹐包括跨音速工况中激波和边界层的相互干涉﹔透平机械特有的边界条件﹐例如週期性条件等。
通常採用柱坐标系 (x﹑y﹑z)来描述透平机械内部的气体流场﹐也就是把速度﹑压力﹑密度和温度等参数视为﹑﹑和时间的函数。若将坐标系与动轮固结在一起﹐坐标系上所观察到的就是工质相对於动轮的运动﹐这种坐标系称为相对坐标系。若将坐标系与地面相固结﹐则称为绝对坐标系。这两种坐标系可以相互转换。
在透平机械内部﹐气体的实际流动非常复杂﹐具有三维和非定常的性质﹐且工质本身又是黏性的可压缩实际气体。描述这种流动的方程有连续方程﹑黏性可压缩气体的运动方程﹑能量方程和实际气体的状态方程等。要準确地求解这类具有 4个自变量的非线性偏微分方程组的初步近似值的问题﹐在数学上尚存在困难。为此﹐必须设法对问题进行合理简化。
20世纪以前﹐透平机械中的气体流动是按照一维流动理论设计计算的。1839年﹐A.J.C.B.de圣维南和L.万策尔第一次导出喷管中可压缩气体的一维等熵流动方程。1894年﹐瑞典工程师拉瓦尔﹐C.G.P.de取得了收缩-扩张喷管(后称拉瓦尔喷管)的专利﹐并将它用於汽轮机。二维流动理论產生於1920年。最初是按孤立机翼理论来设计轴流式压气机(即压缩机)叶片﹐后来又修正了相邻叶片的影响。为提高透平机械性能﹐20世纪初开始发展平面叶栅模型。到20世纪中叶﹐已能计算具有任意形状型线叶栅中的位势流动﹐以及按合理规定的表面压力分布来确定叶片形状。
假设气体在无叶间隙中作轴对称定常流动﹐气体的径向分速为零﹐则可把透平机械中的三维流场人为地分解成无叶间隙中流动参数沿径向的变化和圆柱面内的二维流动。但这种假设具有明显的近似性质﹐对於轮轂比小﹑通道子午扩张角大的透平机械尤为如此。为了使流动模型更接近实际﹐必须发展透平机械的三维流动理论。
1905年﹐H.洛伦茨提出通流理论﹐即无限多叶片理论。这种理论假设叶片数目趋於无限多﹐而叶片厚度趋於无限薄。这样﹐两相邻叶片间的各相对流面的形状与叶片中心面一致﹐且周向变化量趋近於零。实际叶片的作用是通过引入一个假想质量力场的办法来考虑的。这样可求得与叶片中心面相重合的极限流面上的气流的解。50年代初﹐中国科学家吴仲华对通流理论作出改进﹐并提出透平机械三维流动通用理论。这个理论引入S 1和S 2两类相对流面的概念﹐并分别导出了这两类流面流动的基本方程﹐通过这两类流面的适当组合和交替运用﹐就可以把一个实际的三维流动问题分解为两个分别沿著S 1和S 2相对流面的相关的二维流动问题(见图 三维流动通用理论示意图
 )。实际上﹐通常假定S 1流面是一些任意旋成面﹐而在S 2流面族中只取一个称为S 2m的中心流面。这样可得到三维流动的初步近似。
)。实际上﹐通常假定S 1流面是一些任意旋成面﹐而在S 2流面族中只取一个称为S 2m的中心流面。这样可得到三维流动的初步近似。 说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条