2) homotopy category of topological spaces
拓扑空间同伦范畴
3) weak topological category
弱拓扑范畴
5) Finite topological category
有限拓扑范畴
6) direct product of topological spaces
拓扑空间的直积
补充资料：拓扑空间
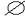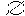| 拓扑空间 topological space 赋予拓扑结构的集合。如果对一个非空集合X给予适当的结构，使之能引入微积分中的极限和连续的概念，这样的结构就称为拓扑，具有拓扑结构的空间称为拓扑空间。引入拓扑结构的方法有多种，如邻域系、开集系、闭集系、闭包系、内部系等不同方法。下面介绍开集系方法。在微积分学中，实一维欧几里得空间R′上的开集具有性质：①任意个开集的并是开集 。②有限个开集的交是开集。③R′及空集  是开集。对任一非空集合X，若X的一个子集族J满足：①J中元的任意并在J中。②J中元的有限交在J中。③X、 在J中，则称J是X的一个拓扑，J中的元称为开集，X连同拓扑J称为一个拓扑空间，记为（X，J）。对任意x∈X，如果Z的子集U包含含有x的一个开集则U称为x的一个邻域。如果X的子集A满足X－A是开集，则称X是闭集。 设X是非空集合，令J0＝｛X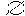，  ｝，称（X，J0）为平庸拓扑空间，J0为平庸拓扑。令J1＝｛A｜AÌX｝，称（X，J1）为离散拓扑空间。在离散拓扑空间中任意子集均是开集。对实数集R1，令J＝｛BÌR1｜"x∈G，∈ε＞0，使（x－ε，x＋ε）ÌG｝，则（R1，J）就是一维欧几里得空间。类似地可定义n维欧几里得空间Rn。设X是拓扑空间，如果X可写为非空开集的分离并，则X称为连通空间；如果对X中任意两点 ，存在X中的道路相连接，则称X为道路连通空间 ；如果X的任意开集作成的覆盖存在有限子覆盖 ，则称X为紧空间；如果X中的任意序列有收敛子列，则称X是列紧空间 ；如果X中任意两点都存在不相交的邻域 ，则称X是豪斯多夫空间（或T2空间）。上面所提连通性，道路连通性、紧性、列紧性、T2性均是拓扑不变性。连通空间上的实值连续函数具有介值性，即若f∶X→R1连续，X是连通空间，r∈（f（x1），f（x2），则存在c∈（x1，x2）（或c∈（x2，x1）），使f（c）＝r。紧空间上的实值连续函数具有最大值、最小值。紧空间上的连续函数一致连续。若AÌRn，则A为紧，当且仅当A是有界闭集。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条