1) log scale


对数标尺
2) logarithmic scale


对数尺;对数标度;对数计算尺
3) alignment scale


对准标尺
4) logarithmic scale


对数度尺
5) logarithmic scale


对数尺度
6) logarithmic scale


对数尺
补充资料:对数
| 对数 logarithm 设a>0,且a≠1,b为任意正实数,如果实数x使等式ax=b成立,就称x为b的以a为底的对数。用记号 logab 表示,即logab =x,a称为对数的底数,b 称为对数的真数。例如,根据幂的等式103=1000,可以说3是以10为底数以 1000为真数的对数,即 log101000=3,同样,由 24=16,就有 log216=4,关系式ax=b与logab=x有一个成立时,另一个也就成立。在两个关系式中,a,b,x三个数的名称对照如下: ax=b logab=x a—幂底数 a—对数底数 b—幂 b—对数真数 x—幂指数 x—对数由于幂永远是正数,所以在对数中,真数只能是正数,又因为任何底数的零次幂总等于1,所以1的对数永远是零。对于固定的底数任何一个正数的对数有且仅有一个。 由给定真数求对数的运算称为对数运算。对数运算有以下法则: 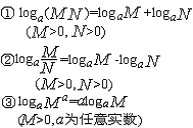 在实用上,常采用以10为底的对数,并将对数记号简写为lgb,称为常用对数,它适用于求十进伯制整数或小数的对数。例如lg10=1,lg100=lg102=2,lg4000=lg(103×4)=3+lg4,可见只要对某一范围的数编制出对数表,便可利用来计算其他十进制数的对数的近似值。在数学理论上一般都用以无理数e=2.7182818……为底的对数,并将记号 loge。简写为ln,称为自然对数,因为自然对数函数的导数表达式特别简洁,所以显出了它比其他对数在理论上的优越性。历史上,数学工作者们编制了多种不同精确度的常用对数表和自然对数表。但随着电子技术的发展,这些数表已逐渐被现代的电子计算工具所取代。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条