1) hyperbolic scale


双曲线比例尺
2) curve scale


曲线比例尺
3) hybrid curve


混合比例尺曲线
4) Bi-scale curve connecting


双比例曲线拼接
5) bar scale


线比例尺
6) track scaling


测井曲线道比例尺
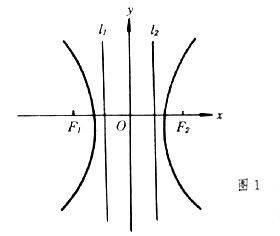
补充资料:双曲线
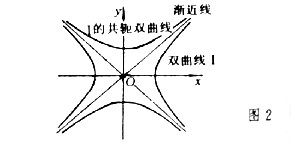
| 双曲线 hyperbola 二次曲线的一种。平面上到两个定点F1、F2的距离之差的绝对值等于一个常数2a的动点的轨迹。定点F1、F2称为双曲线的焦点,两焦点间的距离称为焦距(记为2c)。这个双曲线的标准方程为 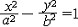 (此处b2=c2-a2)。双曲线有两条互相垂直的对称轴,焦点所在的轴称为实轴,和双曲线不交的轴称为虚轴,分别如图1中的x轴和y轴 。双曲线分为两支,分别位于虚轴的两侧(图1)。标图1准方程中的a,b分别称为双曲线的半实轴长和半虚轴长,a,b相等时,称为等轴双曲线。双曲线有一个对称中心,称为中心,如图1中的坐标原点。双曲线上的动点沿双曲线移向无穷远时,与过中心的两条定直线 (此处b2=c2-a2)。双曲线有两条互相垂直的对称轴,焦点所在的轴称为实轴,和双曲线不交的轴称为虚轴,分别如图1中的x轴和y轴 。双曲线分为两支,分别位于虚轴的两侧(图1)。标图1准方程中的a,b分别称为双曲线的半实轴长和半虚轴长,a,b相等时,称为等轴双曲线。双曲线有一个对称中心,称为中心,如图1中的坐标原点。双曲线上的动点沿双曲线移向无穷远时,与过中心的两条定直线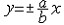 无限接近 ,即距离趋向于零,这两条定直线称为双曲线的渐近线 (图2)。交换双曲线的实轴和虚轴所得的双曲线 无限接近 ,即距离趋向于零,这两条定直线称为双曲线的渐近线 (图2)。交换双曲线的实轴和虚轴所得的双曲线 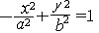 ,称为原来双曲线的共轭双曲线。双曲线和它的共轭双曲线有共同的渐近线(图2)。 双曲线的焦距与实轴长之比 ,称为原来双曲线的共轭双曲线。双曲线和它的共轭双曲线有共同的渐近线(图2)。 双曲线的焦距与实轴长之比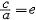 称为双曲线的离心率 。双曲线的离心率大于1,当离心率由小变大时,双曲线开口就由扁狭变得开阔。双曲线也可看成是平面上到定点(焦点)与到定直线(准线)的距离之比(离心率)等于某一大于1的常数的动点的轨迹。双曲线有两条准线(图1),对于焦点F1,相应的准线是l1 ,对于焦点F2,相应的准线是l2 称为双曲线的离心率 。双曲线的离心率大于1,当离心率由小变大时,双曲线开口就由扁狭变得开阔。双曲线也可看成是平面上到定点(焦点)与到定直线(准线)的距离之比(离心率)等于某一大于1的常数的动点的轨迹。双曲线有两条准线(图1),对于焦点F1,相应的准线是l1 ,对于焦点F2,相应的准线是l2
|
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条