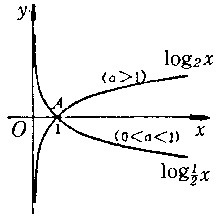1) function
[英]['fʌŋkʃn] [美]['fʌŋkʃən]


函数;作用;功能
2) function
[英]['fʌŋkʃn] [美]['fʌŋkʃən]


功能函数作用
3) function
[英]['fʌŋkʃn] [美]['fʌŋkʃən]


作用,功能,函数
4) function
[英]['fʌŋkʃn] [美]['fʌŋkʃən]


函数,功能,作用,职能
5) function
[英]['fʌŋkʃn] [美]['fʌŋkʃən]


(1)作用,功能(2)函数
6) function
[英]['fʌŋkʃn] [美]['fʌŋkʃən]


n.功能,作用;(pl.)职务;函数 v.起作用
补充资料:函数
| 函数 functions 数学中的一种对应关系,是从某集合A到实数集B的对应。简单地说,甲随着乙变,甲就是乙的函数。精确地说,设X是一个不空集合,Y是某个实数集合,f是个规则,若对X中的每个x,按规则f,有Y中的一个y与之对应,就称f是X上的一个函数,记作y=f(x),称X为函数f(x)的定义域,Y为其值域,x叫做自变量,y为因变量。 例1:y=sinx X=[0,2π],Y=[-1,1],它给出了一个函数关系。当然,把Y改为Y1=(a,b),a<b为任意实数,仍然是一个函数关系。 例2:某商场一年12个月毛线的零售量(单位:百千克)变化,见表1。
例3:某河道的一个断面图如图1所示。
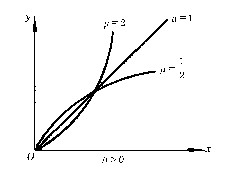
其深度y与一岸边点O到测量点的距离x之间的对应关系呈曲线,这代表一个函数,定义域为[0,b]。以上3例展示了函数的三种表示法:公式法,表格法和图像法。 复合函数 有3个变量,y是u的函数,y=ψ(u),u是x的函数,u=f(x),往往能形成链:y通过中间变量u构成了x的函数: x→u→y,这要看定义域:设ψ的定义域为U。f的值域为U,当U*ÍU时,称f与ψ构成一个复合函数,例如y=lgsinx,x∈(0,π)。此时sinx>0,lgsinx有意义。但如若规定x∈(-π,0),此时sinx<0,lgsinx无意义,就成不了复合函数。 反函数 就关系而言,一般是双向的,函数也如此,设y=f(x)为已知的函数,若对每个y∈Y,有唯一的x∈X,使f(x)=y,这是一个由y找x的过程,即x成了y的函数,记为x=f -1(y)。称f -1为f的反函数。习惯上用x表示自变量,故这个函数仍记为y=f -1(x),例如y=sinx与y=arcsinx互为反函数。在同一坐标系中,y=f(x)与y=f -1(x)的图形关于直线y=x对称。 隐函数 若能由函数方程F(x,y)=0确定y为x的函数y=f(x),即F(x,f(x))≡0,就称y是x的隐函数。 多元函数 设点(x1,x2,…,xn)∈GÍRn,UÍR1,若对每一点(x1,x2,…,xn)∈G,由某规则f有唯一的u∈U与之对应:f:G→U,u=f(x1,x2,…,xn),则称f为一个n元函数,G为定义域,U为值域。 基本初等函数及其图像 幂函数、指数函数、对数函数、三角函数、反三角函数称为基本初等函数。 ①幂函数:y=xμ(μ≠0,μ为任意实数)定义域:μ为正整数时为(-∞,+∞),μ为负整数时是(-∞,0)∪(0,+∞);μ= 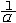 (α为整数),当α是奇数时为(-∞,+∞),当α是偶数时为(0,+∞);μ=p/q,p,q互素,作为 (α为整数),当α是奇数时为(-∞,+∞),当α是偶数时为(0,+∞);μ=p/q,p,q互素,作为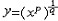 的复合函数进行讨论。略图如图2、图3。 的复合函数进行讨论。略图如图2、图3。
②指数函数:y=ax(a>0,a≠1),定义成为(-∞,+∞),值域为(0,+∞),a>0时是严格单调增加的函数(即当x2>x1时, 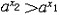 ),0<a<1时是严格单减函数。对任何a,图像均过点(0,1),注意y=ax和y=( ),0<a<1时是严格单减函数。对任何a,图像均过点(0,1),注意y=ax和y=(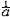 )x的图形关于y轴对称。如图4。 )x的图形关于y轴对称。如图4。
③对数函数:y=logax(a>0),称a为底,定义域为(0,+∞),值域为(-∞,+∞)。a>1时是严格单调增加的,0<a<1时是严格单减的。不论a为何值,对数函数的图形均过点(1,0),对数函数与指数函数互为反函数。如图5。
④三角函数:见表2。
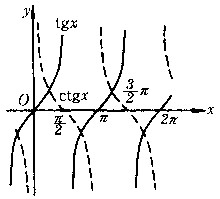
正弦函数、余弦函数如图6,图7所示。
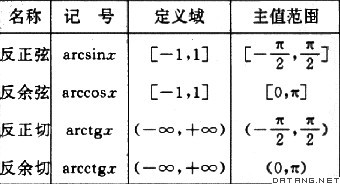
⑤反三角函数:见表3。双曲正、余弦如图8。
⑥双曲函数:双曲正弦 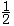 (ex-e-x),双曲余弦(ex+e-x),双曲正切(ex-e-x)/(ex+e-x),双曲余切(ex+e-x)/(ex-e-x)。 (ex-e-x),双曲余弦(ex+e-x),双曲正切(ex-e-x)/(ex+e-x),双曲余切(ex+e-x)/(ex-e-x)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条