1) mass center integral


质心积分
2) cardiointegram


心电积分
3) particle integral


质点积分
4) integral property


积分性质
1.
An integral property of the convex function is generalized,and the some integral inequalities of the convex function are given.
给出了凸函数的一个积分性质的推广,并由此得到了凸函数的几个积分不等式。
2.
Through generalized Fourier transform,Fourier transform s differential property and integral property,the problem of how to explain generalized Fourier transform of unit step function is discussed.
通过广义Fourier变换、Fourier变换的积分性质、微分性质等来讨论单位阶跃函数的广义Fourier变换的求解问题。
3.
This paper,by using the method of generalized function,discusses the shielded effect on a type of functions in generalized Fourier transform,proves the integral property of the image function in generalized Fourier transform and also provides the calculation formula and applications of the same.
利用广义函数方法,探讨了一类函数在广义Fourier变换下的屏蔽效应,证明了广义Fourier变换的象函数的积分性质,并给出了计算公式和应用示例。
5) Quermassintegrals


均质积分
1.
On Brunn-Minkowski Inequality for the Quermassintegrals and Dual Quermassintegrals of L_p-Projection Body;
L_p-投影体的均质积分和对偶均质积分的Brunn-Minkowski不等式
6) distribution centroid


分布质心
补充资料:质心
| 质心 mass,centre of 质点系质量分布的平均位置。质量中心的简称。它同作用于质点系上的力系无关。设n个质点组成的质点系,其各质点的质量分别为m1,m2,…,mn。若用r1,r2,…,rn分别表示质点系中各质点相对某固定点的矢径,rc表示质心的矢径,则有rc=  miri/ miri/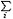 mi。当物体具有连续分布的质量时,质心C的矢径rc= mi。当物体具有连续分布的质量时,质心C的矢径rc= ρrdτ/ ρrdτ/ ρdτ,式中ρ为体(或面、线)密度;dτ为相当于ρ的体(或面、线)元;积分在具有分布密度ρ的整个物质体(或面、线)上进行。由牛顿运动定律或质点系的动量定理,可推导出质心运动定理:质心的运动和一个位于质心的质点的运动相同,该质点的质量等于质点系的总质量,而该质点上的作用力则等于作用于质点系上的所有外力平移到这一点后的矢量和。由这个定理可推知:①质点系的内力不能影响质心的运动。②若质点系所受外力的主矢始终为零, 则其质心作匀速直线运动或保持 静止状态。③若作用于质点系上外力的主矢在某一轴上的投影始终为零,则质心在该轴上的坐标匀速变化或保持不变。质点系的任何运动一般都可分解为质心的平动和相对于质心的运动。质点系相对某一静止坐标系的动能等于质心的动能和质点系相对随质心作平动的参考系运动的动能之和。质心位置在工程上有重要意义,例如要使起重机保持稳定,其质心位置应满足一定条件;飞机、轮船、车辆等的运动稳定性也与质心位置密切相关;此外,若高速转动飞轮的质心不在转动轴线上,则会引起剧烈振动而影响机器正常工作和寿命。 ρdτ,式中ρ为体(或面、线)密度;dτ为相当于ρ的体(或面、线)元;积分在具有分布密度ρ的整个物质体(或面、线)上进行。由牛顿运动定律或质点系的动量定理,可推导出质心运动定理:质心的运动和一个位于质心的质点的运动相同,该质点的质量等于质点系的总质量,而该质点上的作用力则等于作用于质点系上的所有外力平移到这一点后的矢量和。由这个定理可推知:①质点系的内力不能影响质心的运动。②若质点系所受外力的主矢始终为零, 则其质心作匀速直线运动或保持 静止状态。③若作用于质点系上外力的主矢在某一轴上的投影始终为零,则质心在该轴上的坐标匀速变化或保持不变。质点系的任何运动一般都可分解为质心的平动和相对于质心的运动。质点系相对某一静止坐标系的动能等于质心的动能和质点系相对随质心作平动的参考系运动的动能之和。质心位置在工程上有重要意义,例如要使起重机保持稳定,其质心位置应满足一定条件;飞机、轮船、车辆等的运动稳定性也与质心位置密切相关;此外,若高速转动飞轮的质心不在转动轴线上,则会引起剧烈振动而影响机器正常工作和寿命。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条