1) free surface effect


自由液面效应
2) effect of surface free energy difference of solid and falling fluid


固液表面自由能差效应
3) free-surface effect


自由面效应
4) free surface effect


自由表面效应
5) free surface


自由液面
1.
The changes of free surface shape of TiAl-based melt during induction melting with cold crucible;
TiAl基合金感应熔炼自由液面的变化规律研究
2.
Numerical research on pressure distribution of inside wall of a cave-in cavity with free surface under the uniform fluid condition;
均匀流场中含自由液面的陷落腔压力分布数值研究
3.
Numerical study of the three-dimensional free surface in cylindrical tank;


贮腔类三维自由液面动力学问题数值研究
补充资料:液体自由表面波
| 液体自由表面波 liquid,free surface waves in 液体自由表面受扰后出现的此起彼伏的波浪运动。液体自由表面是指江河湖海和开口容器中的液体等接触大气的液面。静止液体自由表面是水平的,受扰后液体质点离开其平衡位置,同时重力和表面张力发挥回复力作用促其返回平衡位置,然后质点在惯性作用下继续向另一侧运动,从而形成液体质点的振动和因振动传播而产生的自由表面波。若波长比波高大得多,则自由表面的曲率很小,表面张力也很小,可忽略其作用,只考虑重力,这种液体自由表面波称为重力波。反之,若波长极短,则自由表面曲率很大,表面张力也很大,可忽略重力作用,只考虑表面张力,这种波称为毛细波或涟波,其波长在1~2厘米之间。微风吹皱的一湖春水就是毛细波的一例。液体自由表面波的要素同波的要素基本一致。波速依赖于波长的称弥散波,如深水重力波、毛细波等;波速与波长无关的称非弥散波,如浅水重力波。小振幅波的波速为 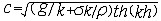 ,式中h为液深;σ为表面张力;ρ为液体密度;k为波数;g为重力加速度。对毛细波,只考虑表面张力作用, ,式中h为液深;σ为表面张力;ρ为液体密度;k为波数;g为重力加速度。对毛细波,只考虑表面张力作用,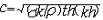 。对重力波,只考虑重力作用, 。对重力波,只考虑重力作用, ;无限水深时, ;无限水深时, ;浅水时,kh1,th(kh)≈kh, ;浅水时,kh1,th(kh)≈kh,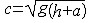 。在有限振幅波中,斯托克斯波的波速为c=(g/k) 。在有限振幅波中,斯托克斯波的波速为c=(g/k)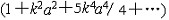 ,式中a为波幅。孤立波的波速 ,式中a为波幅。孤立波的波速  ,式中h为无波时静止液面的水深。许多单个波组成的波群的传播速度称为群速。若干波幅和周期都很接近的进行波叠加后形成波列,波列的包络称为波包。波包包络许多单个波,又称波群(图1),波群的波长比其中单个波的波长大得多 。群速cg同波速c的关系由瑞利公式给出: ,式中h为无波时静止液面的水深。许多单个波组成的波群的传播速度称为群速。若干波幅和周期都很接近的进行波叠加后形成波列,波列的包络称为波包。波包包络许多单个波,又称波群(图1),波群的波长比其中单个波的波长大得多 。群速cg同波速c的关系由瑞利公式给出: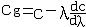 ,式中λ为波长。弥散波的群速不等于波速,例如深水重力波的群速等于其波速的一半;毛细波的群速为波速的3/2倍。非弥散波的群速同波速相等。群速也是波能量的传播速度。 ,式中λ为波长。弥散波的群速不等于波速,例如深水重力波的群速等于其波速的一半;毛细波的群速为波速的3/2倍。非弥散波的群速同波速相等。群速也是波能量的传播速度。
进行波 有空间和平面进行波,前者沿液面各方向传播,波幅随传播距离而减小;后者沿某一方向传播,波幅为常量。常见的一种平面进行波是小振幅规则进行波,其波形可表示为ζ=asin(kx-ωt) ,式中ζ为液体自由表面质点离开其平衡位置的位移,a为波幅,k为波数,ω为振动角频率(图2)。小振幅平面进行波是线性波,它在一个波长λ内的总能量为常值ρga2λ/2其中动能和势能各占一半。研究船舶在波浪中的运动,常采用小振幅规则平面进行波模型。
驻波 波幅随时间周期性变化,波峰、波谷和其他各相位点位置不变的液体自由表面波。驻波有依坐标周期性变化的波幅和固定不动的波节。驻波中的液体质点以各自平衡位置为中心作往复直线运动。质点轨迹直线在波峰和波谷处垂直于水平方向,随着向波节靠近,轨迹直线同水平夹角逐渐变小,至波节处变为水平。质点的振幅随质点深度的增加而迅速递减。平面驻波在一个波长λ内的总能量为常值ρga2λ/4。驻波主要发生在受限制水域。研究驻波产生的条件,特别是发生共振时的危险环境条件,可预报水库、容器中的动力载荷,以便在工程设计中预加防范。 斯托克斯波 一种无旋的非线性液体自由表面波,是G.G.斯托克斯1847年最先用摄动法在无限深液体重力波中求解出来的。这种波的波峰较尖,波谷较平坦(图3)。与线性波不同,斯托克斯波的波速受波幅影响。其各分量波之间相互干扰并产生新的分量波,在共振条件下,新波不断从原型波中吸收能量使自身波幅不断增长,因而存在不稳定性。用斯托克斯波作为环境条件计算海洋结构物所受的波浪力更符合实际情况,其结果与线性波有较大差异。
孤立波 仅有一个孤立波峰的非线性波(图4)。孤立波在传播过程中保持固定波形,理论波长为无限大。其波形为  ,式中h为平衡时的水深;坐标系Oxy是随波行进的。当a≈h时,波形不稳定并产生碎波。孤立波是一种实际存在的波,已被用作一种环境条件来计算海洋结构物的载荷和响应。浅水航道中大平底船的运动或河流中来流速度的突然变化都会产生孤立波。 ,式中h为平衡时的水深;坐标系Oxy是随波行进的。当a≈h时,波形不稳定并产生碎波。孤立波是一种实际存在的波,已被用作一种环境条件来计算海洋结构物的载荷和响应。浅水航道中大平底船的运动或河流中来流速度的突然变化都会产生孤立波。
椭圆余弦波 以椭圆余弦函数表示的有限深渠道中的非线性波。其波形为y=h2+(h1-h2)cn2(x/β),式中x为水平方向横坐标;h1和h2为波峰和波谷的纵坐标值;β为一参量,同波速、水深、h1和h2有关。当水深与波长之比在1/50~1/10范围内,可用椭圆余弦波来计算其对海洋结构物的载荷。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条



