1) acceleration
[英][ək,selə'reɪʃn] [美][ək'sɛlə'reʃən]


加速度;增量;高潮间隙的缩减
2) priming
[英]['praimiŋ] [美]['praɪmɪŋ]


沸溅;高潮间隙的缩减;灌注;底漆
4) Acceleration of deweighting


减量加速度
5) increase the time to reduce velocity


增加减速时间
6) acceleration increasement


加速度增量
1.
The formulae of follower linear displacement error,extra velocity and acceleration increasements were derived.
给出了由滚子半径误差和凸轮轮廓几何误差引起的从动件位移误差、附加速度增量和加速度增量的计算公式。
补充资料:加速度
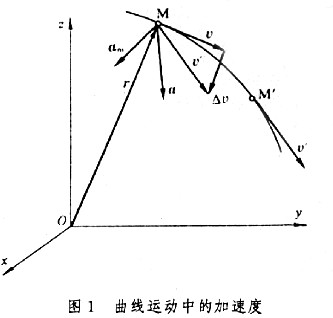
| 加速度 acceleration 描述动点在某瞬时的速度(包括大小和方向)变化率的矢量,记为a。 点在直线运动中的加速度 点作直线运动时,其位移、速度和加速度只有正负两个方向,可用代数量s 、v 、a表示。取Ox轴与运动轨迹重合。设某一时刻 t,点在轨迹上的位置为M,相应的坐标为x,速度为v。x和v都是时间t的函数。又设点在时刻t′的速度为v′,则 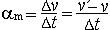 表示点的速度在Δt 时间内的平均变化率,称为该段时间点的平均加速度。当Δt→0时,am的极限a表示点在时刻t的速度变化率,称为点的加速度, 表示点的速度在Δt 时间内的平均变化率,称为该段时间点的平均加速度。当Δt→0时,am的极限a表示点在时刻t的速度变化率,称为点的加速度,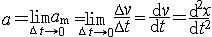 。a>0时,点的加速度沿Ox轴方向;a<0时,加速度与Ox轴方向相反。 。a>0时,点的加速度沿Ox轴方向;a<0时,加速度与Ox轴方向相反。点在曲线运动中的加速度 设点在某一参考系(如直角坐标系Oxyz,图1)中的轨迹是一条空间曲线,则在任一时刻t,点在轨迹上的位置矢量r可用矢量方程r=r(t)表示。设在时刻t和t′,点在轨迹上的位置( 图1)分别为M和M′,相应的速度矢量为v和v′,则 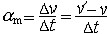 表示在Δt时间内,点的速度的平均变化率,称为平均加速度。当Δt→0时,am的极限 a 表示点在时刻t的速度变化率 表示在Δt时间内,点的速度的平均变化率,称为平均加速度。当Δt→0时,am的极限 a 表示点在时刻t的速度变化率,称为点的加速度 。 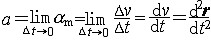 。轨迹曲线上任一点都有一个密切面和法平面,时刻t点的加速度 a在轨迹曲线上M点的密切面内,并指向轨迹凹侧。 。轨迹曲线上任一点都有一个密切面和法平面,时刻t点的加速度 a在轨迹曲线上M点的密切面内,并指向轨迹凹侧。
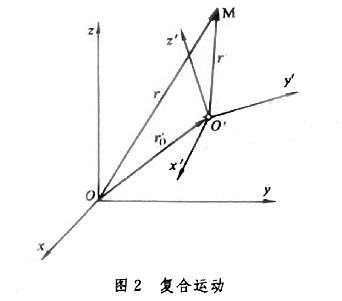
① 切向加速度。描述作曲线运动的点在某瞬时速度大小(速率)变化率的矢量,记为aτ。其方向沿轨迹各点的切向,即 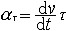 ,τ为沿轨迹各点的切向单位矢量。当dv/dt和v同号时,点作加速运动;反之,点作减速运动。 ,τ为沿轨迹各点的切向单位矢量。当dv/dt和v同号时,点作加速运动;反之,点作减速运动。②法向加速度。描述作曲线运动的点在某瞬时速度方向变化率的矢量,记为an。其方向沿曲线轨迹各点的主法线方向指向曲率中心 ,大小等于速率 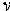 的平方除以曲率半径ρ ,即 的平方除以曲率半径ρ ,即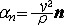 ,n为沿轨迹各点的主法向单位矢量。若 v、ρ不变,则an的大小不变,方向恒指向圆心,点作匀速圆周运动;若ρ=∞,则an=0,点作直线运动。 ,n为沿轨迹各点的主法向单位矢量。若 v、ρ不变,则an的大小不变,方向恒指向圆心,点作匀速圆周运动;若ρ=∞,则an=0,点作直线运动。 由此可见,点作曲线运动的加速度可以分解为切向加速度aτ和法向加速度an,即 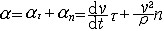 。于是,加速度的大小 。于是,加速度的大小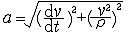 ,方向可由 a对切线方向τ和主法线方向n的夹角的方向余弦决定。 ,方向可由 a对切线方向τ和主法线方向n的夹角的方向余弦决定。点在复合运动中的加速度 点的复合运动是指动点对运动参考系的相对运动同运动参考系上与动点重合之点的运动(即动点的牵连运动)的合成运动(即动点的绝对运动)。 ①相对加速度。设点相对于参考系Οxyz运动,而另一参考系O′x′y′z′也相对于Oxyz运动,则称Oxyz为静止参考系,O′x′y′z′为运动参考系(图2)。点的相对加速度是点对运动参考系的加速度,记为 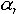 。 。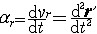 ,式中 ,式中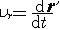 表示相对速度,r′表示某时刻t点M相对于O′x′y′z′的矢径。 表示相对速度,r′表示某时刻t点M相对于O′x′y′z′的矢径。
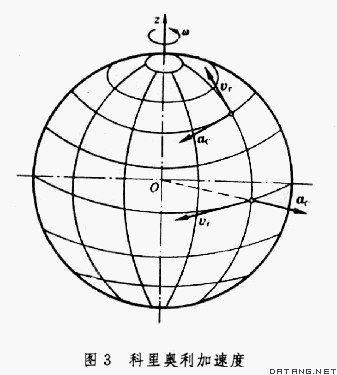
②牵连加速度。点固结在运动参考系中,随此参考系运动而具有的加速度,记为 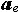 。 。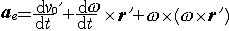 ,式中 ,式中 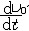 为平动牵连加速度,表示运动在参考系随坐标原点O'平动时点M所具有的加速度; 为平动牵连加速度,表示运动在参考系随坐标原点O'平动时点M所具有的加速度;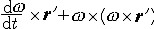 为转动牵连加速度,表示运动参考系作为刚体绕O'点运动时,点所具有的加速度。ω表示运动参照系在瞬时t的角速度。 为转动牵连加速度,表示运动参考系作为刚体绕O'点运动时,点所具有的加速度。ω表示运动参照系在瞬时t的角速度。③科里奥利加速度,由于点的相对运动和运动参考系的牵连运动相互影响而引起的附加加速度,记为 ac。ac=2ω×υr。例如 ,由于地球绕地轴转动,地面上物体相对地球运动时只要其相对速度方向不和地轴平行 ,此物体就有科里奥利加速度,沿地球经线或纬线运动的物体都有科里奥利加速度ac(图3)。 ④加速度的合成。点在复合运动中的加速度a(即绝对加速度),等于相对加速度ar,牵连加速度ae及科里奥利加速度ac的矢量和,即a= ar +ae +ac。这就是加速度合成定理。加速度的量纲为LT -2,它的SI单位为m/s2。
|
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条