1) damped harmonic oscillator


阻尼简谐振子
2) damped harmonic oscillator


阻尼谐振子
1.
The Lagrangian and Hamiltonian of damped harmonic oscillator


阻尼谐振子的拉格朗日函数和哈密顿函数
2.
A damped harmonic oscillator without a driving force was studied using canonical tramsformation;An exact wavefunction and energy level for the damped harmonic oscillator has Been obtained.
对于无外界驱动力且阻力与速度成正比的阻尼谐振子,通过正则变换,得出了阻尼谐振子的严格波函数及其相应能级。
3.
Mesoscopic series-parallel connection RLC circuit is quantized by the method of damped harmonic oscillator operation.
将介观串并联RLC电路等效成阻尼谐振子并量子化,研究了压缩真空态的激发态、压缩真空态、真空态下电流和电压的量子涨落。
3) damping harmonic oscillator


阻尼谐振子
1.
The Schrdinger equation is given directly from the classical Hamiltonian function of a damping harmonic oscillator,and its solution is obtained by the separation of variables.
写出阻尼谐振子的哈密顿函数,对其直接量子化,用分离变量法得出了薛定谔方程的解。
4) damped non-harmonic vibration


阻尼非简谐振动
5) simple harmonic oscillation with damping


阻尼简谐振动
1.
The impacted bridge was considered to do simple harmonic oscillation with damping after impact.
认为桥梁在受到撞击后做阻尼简谐振动,提出了如等效振幅、等效弹性系数等概念。
补充资料:简谐振动
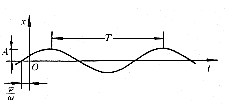
| 简谐振动 simple harmonic vibration 描述系统状态的物理量随时间按正弦或余弦规律作周期性变化的过程。又称简谐运动。作简谐振动的物体的加速度始终同它的位移成正比,但方向相反。即x=-ω2x, 式中ω2为比例常量。作简谐运动的物体,其运动规律可表达为: x=Asin(ωt+ 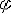 ) )=Asin(2πt/T+ 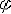 ) )=Asin(2πf t+ 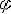 ) )式中x为位移;A为振幅;ω为角(圆)频率;t为时间;T为周期;f 为频率;ωt+ 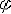 为相位 ; 为相位 ;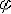 为初相位(见图)。这种运动对其平衡位置(零点)是对称的。在零点上,物体速度最大,加速度为零;在最大位移处(转向点),速度为零,加速度最大。简谐运动是最简单、最基本的振动形式;任何周期振动都可由许多不同频率和振幅的简谐运动合成。简谐运动是单自由度无阻尼系统微幅自由振动的抽象模型。悬挂在弹簧下端物体的微幅振动,扭摆的微幅振动以及晶体中原子围绕平衡位置的微幅振动都可近似地看作简谐振动。 为初相位(见图)。这种运动对其平衡位置(零点)是对称的。在零点上,物体速度最大,加速度为零;在最大位移处(转向点),速度为零,加速度最大。简谐运动是最简单、最基本的振动形式;任何周期振动都可由许多不同频率和振幅的简谐运动合成。简谐运动是单自由度无阻尼系统微幅自由振动的抽象模型。悬挂在弹簧下端物体的微幅振动,扭摆的微幅振动以及晶体中原子围绕平衡位置的微幅振动都可近似地看作简谐振动。
|
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条